2019年大学入試センター試験数学1A「第2問データの分析（データの変換）」を解いてみる。

2019年2月14日2023年1月14日データの分析,大学入試センター試験実用数学技能検定（数学検定数検),数検準2級

読了時間: 約4分49秒

問題

(3)　一般に$ \ n \ $個の数値$ \ x_1 \ , \ x_2 \ , \ \cdots \ , \ x_n \ $からなるデータ$ \ X \ $の平均値を$ \ \overline{x} \ $,分散を$ \ s^2 \ $,標準偏差を$ \ s \ $とする。各$ \ x_i \ $に対して

$ \ x_i’=\frac{x_i-\overline{x}}{s} \ $
と変換した$ \ x_1′ \ , \ x_2′ \ , \ \cdots \ , \ x_n’ \ $をデータ$ \ X’ \ $とする。
ただし,$ \ n \geq 2 \ , \ s \gt 0 \ $として以下の問いに答えよ。

$$\begin{align}・\quad X&の偏差x_1-\overline{x} \ , \ x_2-\overline{x} \ , \ \cdots \ , \ x_n-\overline{x} \ , \ の平均値は\\\\ & \ \color{#0004fc}{テ}\quad である。 \\\\・\quad X’&の平均値は \ \color{#0004fc}{ト}\quad である。 \\\\ ・\quad X’&の標準偏差は \ \color{#0004fc}{ナ}\quad である。 \end{align}$$

準備

$$\begin{align}平均\quad \quad \overline{x}=&\frac{1}{n}\sum_{i=1}^{n}{x_i} \\\\ 分散\quad \quad s^2=&\frac{1}{n}\sum_{i=1}^{n}{\left( x_i-\overline{x}\right)^2} \end{align}$$

Xの偏差の平均値を求める。（テ）

$$\begin{align}\frac{1}{n}\sum_{i=1}^{n}{\left( x_i-\overline{x}\right)}=&\frac{1}{n}\sum_{i=1}^{n}{x_i}-\frac{n\overline{x}}{n} \\\\ =&\overline{x}-\overline{x}\\\\ =&\color{#0004fc}{0} \end{align}$$

X’の平均値を求める。（ト）

$$\begin{align}\overline{X’}=&\frac{1}{n}\sum_{i=1}^{n}{x_i’} \\\\ =&\frac{1}{n}\sum_{i=1}^{n}{\sqrt{\frac{\left( x_i-\overline{x}\right)^2}{s^2}}} \\\\ =&\frac{1}{s}\cdot \frac{1}{n}\sum_{i=1}^{n}{\left( x_i-\overline{x}\right)}=\frac{1}{s}\cdot 0\\\\ =&\color{#0004fc}{0} \end{align}$$

X’の標準偏差を求める。（ナ）

$$\begin{align}X’の分散を&s’^2とし, \ X’の標準偏差を&s’とする。 \end{align}$$ $$\begin{align}s’^2=&\frac{1}{n}\sum_{i=1}^{n}{\left( x_i’-\overline{X’}\right)^2} \\\\ ここで&\overline{X’}=0より \\\\ 与式=&\frac{1}{n}\sum_{i=1}^{n}{x_i’^2}\\\\ =&\frac{1}{n}\sum_{i=1}^{n}{\frac{\left( x_i-\overline{x}\right)^2}{s^2}}\\\\ ここで&\frac{1}{n}\sum_{i=1}^{n}{\left( x_i-\overline{x}\right)^2}=s^2\quad より\\\\ 与式=&\frac{s^2}{s^2}=1\ s’ \gt 0\quad より\\\\ s’=&\color{#0004fc}{1} \end{align}$$

ここからは参考程度に。（ニ）

Lukia

最後の問題は、説明としては不正確かもしれません。
それでも参考程度にはなるから読んでみよう。という方のみ、読み進めてください。また、こたえ自体は正しいものを載せていますので、御安心を。

問題

図4で示されたモンシロチョウの初見日のデータ$ \ M \ $とツバメの初見日のデータ$ \ T \ $について上の変換を行ったデータを$ \ M’ \ , \ T’ \ $とする。
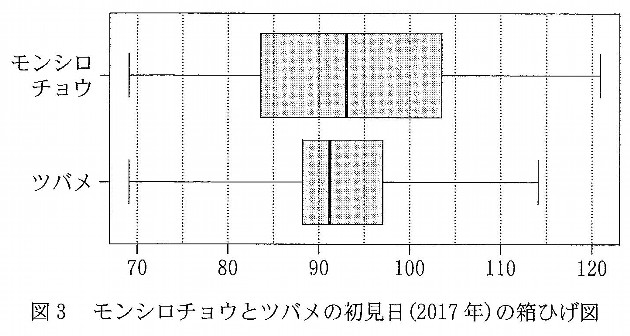
次の「ニ」に当てはまる図を、図5の⓪～③のうちから一つ選べ。変換後のモンシロチョウの初見日のデータ$ \ M’ \ $と変換後のツバメの初見日のデータ$ \ T’ \ $の散布図は,$ \ M’ \ $と$ \ T’ \ $の標準偏差の値を考慮すると$ \ \color{#0004fc}{ニ} \ $である。

Lukia

データ$ \ x_i \ $を$ \ x_i’ \ $に変換して、
「あれこれいじり」ましたが、標準偏差が$ \ 1 \ $とかなり小さい値に落ち着いたので、散布図のばらつきにさほど変化はなさそうです。
というわけで、図4に近い散布図⓪か、散布図②にしぼられます。

Lukia

図3の箱ひげ図を見ると、第二四分位数がモンシロチョウもツバメも90日を超えています。

Lukia

この第二四分位数を図5の0とみなすと、モンシロチョウの軸では右方向にスライドし、同様にツバメの軸も上方向にスライドします。
つまり、散布図全体としては、右上に移動することになります。

Lukia

そして、最後に、標準偏差が小さかったので、原点を通り、傾き$ \ 1 \ $の直線上に存在する点の数も変わらないと考えられます。実際に線を引いてみると、線の付近に「少なくとも」4点が存在していることがわかります。
ゆえに、以上の考えに合致する散布図は、②となります。

過去問にあたって、傾向をつかんでおきましょう。

Lukia

当記事で取り扱ったような、データを変換して、それが元のデータと、どこが違って、どこが同じか。というのを考えさせるような問題は、大学入試センター試験が大好きな問題のひとつです。
問題のページ数は相当ありますが、大問2の一部に過ぎないので、そんなに時間をかける余裕はないと思います。ゆえに、できれば早くから過去問に触れて、どういう傾向かとか、データを変換することによって、変わるもの、変わらないものを覚えてしまうのもよいと思います。
センター試験の過去問以外には、模試の過去問集などにも実践的な問題がありますので、とにかく数多く当たって、時短のポイントを探っておきましょう。

2019年大学入試センター試験の数学の問題の一覧です。