高校数学の「外分比がらみの平面ベクトル」に関する問題を解いてみる。(Yahoo!知恵袋より)

(1) \( \ \overrightarrow{\mathrm{OP}} \ \)を,\( \ \overrightarrow{\mathrm{OA}} \ \)と\( \ \overrightarrow{\mathrm{OB}} \ \)を用いて表せ.
(2) 内積\( \ \overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}} \ \)の値を求めよ.
(3) \( \ \mathrm{Q} \ \)を辺\( \ \mathrm{OB} \ \)上の動点とする.内積\( \ \overrightarrow{\mathrm{PQ}}\cdot \overrightarrow{\mathrm{AQ}} \ \)が最小となるときの\( \ \mathrm{\frac{OQ}{QB}} \ \)の値と,内積の最小値を求めよ.

Lukia
「イメージしにくくて苦手・・・」と思う方もいらっしゃると思います。(私もそうです。)
でも、そんなときは無理しない。
図を描け。と言われているわけではないので、内分と同じように扱えばいいんです。
外分比も内分比と同じように扱える。(ただしコツあり)

Lukia
辺\( \ \mathrm{AB} \ \)を\( \ \color{#0004fc}{3:-1} \ \)に内分するように、「内分比」を互い違いにおいてやります。
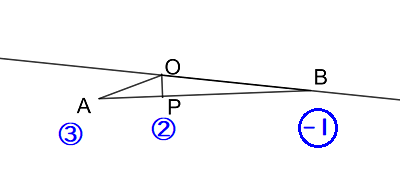

Lukia
$$\begin{align}\overrightarrow{\mathrm{OP}}=&\frac{1}{2}\left( 3\overrightarrow{\mathrm{OA}}-\overrightarrow{\mathrm{OB}}\right) \end{align}$$
内積を求めよう。
$$\begin{align}\mathrm{OP}\perp\mathrm{AB}&\quad より \\\\ \overrightarrow{\mathrm{OP}}\cdot \overrightarrow{\mathrm{AB}}=&0 \\\\ \frac{1}{2}\left( 3\overrightarrow{\mathrm{OA}}-\overrightarrow{\mathrm{OB}}\right)\left( \overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}}\right)=&0\\\\ 3\overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}}-6-20+\overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}}=&0 \\\\ 4\overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}}=&32\\\\ \\\\ \overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}}=&8 \end{align}$$
ベクトルの内積計算は、とにかく無理しない。
$$\begin{align}\overrightarrow{\mathrm{OQ}}=&k\overrightarrow{\mathrm{OB}}\quad \left( k \ は実数\right)\quad とする.\\\\ \\\\ \overrightarrow{\mathrm{PQ}}\cdot \overrightarrow{\mathrm{AQ}}=&\left( k\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OP}}\right)\left( k\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}}\right) \\\\ =&\left( k\overrightarrow{\mathrm{OB}}-\frac{3}{2}\overrightarrow{\mathrm{OA}}+\frac{1}{2}\overrightarrow{\mathrm{OB}}\right)\left( k\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}}\right) \end{align}$$

Lukia
下のような表を描いて、まずはかけ算し、最終的にたし算していけば、内積が求められます。

$$\begin{align}\overrightarrow{\mathrm{PQ}}\cdot \overrightarrow{\mathrm{AQ}}=&20k^2-10k-2 \\\\ k=&\frac{1}{4}\quad のとき \\\\ \overrightarrow{\mathrm{PQ}}\cdot \overrightarrow{\mathrm{AQ}}& \ は最小値 \ -\frac{13}{4}\quad をとる. \end{align}$$
また,
$$\begin{align}\frac{\mathrm{OQ}}{\mathrm{OB}}=\frac{\vert k\overrightarrow{\mathrm{OB}} \vert}{\vert \overrightarrow{\mathrm{OB}}-k\overrightarrow{\mathrm{OB}} \vert}=&\frac{k}{1-k}\vert \overrightarrow{\mathrm{OB}} \vert \\\\ =&\frac{-\frac{13}{4}}{1+\frac{13}{4}}\cdot 2\sqrt{5} \\\\ =&\frac{26}{17}\sqrt{5} \end{align}$$
こたえ
$$\begin{align}(1)&\quad \quad \overrightarrow{\mathrm{OP}}=\frac{1}{2}\left( 3\overrightarrow{\mathrm{OA}}-\overrightarrow{\mathrm{OB}}\right)\\\\(2)&\quad \quad \overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}}=8\\\\
(3)&\quad \quad 内積の最小値:-\frac{13}{4}\\\\ &\quad \quad \frac{\mathrm{OQ}}{\mathrm{OB}}=\frac{26}{17}\sqrt{5}
\end{align}$$
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません