高校数学の「データの分析（定義・キャタピラー表）」に関する問題を解いてみる。（Yahoo!知恵袋より）

2019年2月12日2023年1月14日データの分析実用数学技能検定（数学検定数検),数検準2級

読了時間: 約5分53秒

[mathjax]

問題

次のデータは,7人の生徒の右手の握力の記録である。
29 , 20 , 21 , 30 , 24 , 19 , 25 (kg)
(1) 各値の偏差の二乗の和を求めよ。
(2) このデータの分散,標準偏差を求めよ。

Lukia

データの分析のところは、正確な計算力がものをいいます。
しかし、やみくもに計算すると、ちょっとしたことでつまずいたり、パニくったりするおそれもあります。
そこで、「キャタピラー方式」を考えてみましたので、その方法を提案してみます。
また、会話形式のほうがわかりやすいと思うので、高校生のペルソナ、れもんさんに登場してもらいます。

仮平均を定めてキャタピラー表を作成する。

Lukia

まずは、なんとなくキリがいいので、$ \ 25 \ $を仮平均としてみます。

Lukia

すると、上は$ \ 30 \ $,下は$ \ 19 \ $ですので、
$ \ 25 \ $との距離の最大は6ということになりますね。
そこで、絶対値を用いて、仮平均と個々のデータとの差を表にしていきます。

$$絶対値\quad \quad 0\quad \quad 1\quad \quad 2\quad \quad 3\quad \quad 4\quad \quad 5\quad \quad 6$$

れもん

これに、どうやって数字を書き込むんですか？

Lukia

絶対値を挟んで、上がプラスのもの、下がマイナスのものとします。

Lukia

データが左から並んでいる順番にやってみましょう。
まず、$ \ 29 \ $ですね。これは、$ \ 29-25=+4 \ $ですので、絶対値$ \ 4 \ $の上に正の字の一として書き込みます。

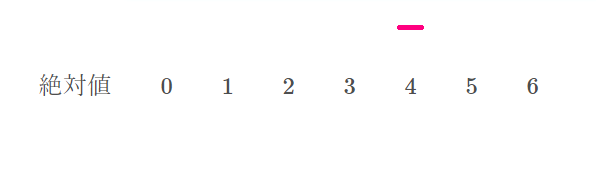
れもん

なるほど。じゃ、次の$ \ 20 \ $は、$ \ 20-25=-5 \ $だから、
絶対値$ \ 5 \ $の下に正の字の一を書くわけですね？

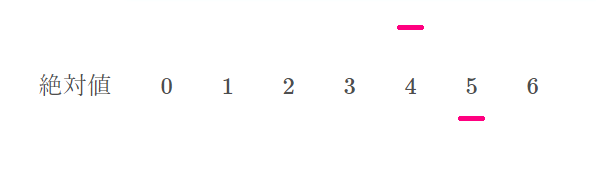
Lukia

その通りです。
それでは、残りの五つのデータもお願いできますか？

れもん

はい。
$ \ 21 \ $は絶対値$ \ 4 \ $の下に一
$ \ 30 \ $は絶対値$ \ 5 \ $の上に一
$ \ 24 \ $は絶対値$ \ 1 \ $の下に一
$ \ 19 \ $は絶対値$ \ 6 \ $の下に一　です。

れもん

あ、でも、$ \ 25 \ $は？

Lukia

$ \ 25 \ $は仮平均そのものなので、まず$ \ 0 \ $なのですが、
まぁ、プラスもマイナスもないですよね。
キャタピラーの回る方向が時計回りなので、便宜上絶対値$ \ 0 \ $の上に一としておいてください。

れもん

はーい。
じゃ、以下のような表になりますね。

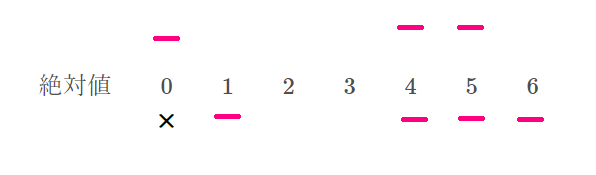
Lukia

7人のデータが絶対値を挟んで上下に振り分けられたわけですが、
上下に同じ数あるものは、当然相殺されて$ \ 0 \ $になりますよね？

れもん

絶対値$ \ 4 \ $つまり、$ \ +4 \ $の人と$ \ -4 \ $の人がいるから、合わせて$ \ 2 \ $で割ると・・・いや、$ \ 0 \ $だから割れないですね。

Lukia

同様のことが絶対値$ \ 5 \ $でもいえます。
つまり相殺できずに残った値の和を求め、それを7で割って、仮平均に加えれば、正しい平均がわかりますね。

れもん

どれどれ・・・
$ \ \frac{0+\left( -1\right)+\left( -6\right)}{7}+25=-1+25=24 \ $

れもん

あっ、正しい平均の値は、$ \ 24 \ $ですね！

Lukia

そのとおりです。
私も、これまで、縦長の数直線を書いたりしてきたのですが、数学の問題で、縦長のスペースを見つけるのは結構難しいんですよね。
そこで、横長にして、絶対値をはさんで上下にデータを振り分けたら、簡単に計算できるようになったので、
これはいい。と。
自分の受験が終わってから気が付くんですから、おとぼけさんもいいとこですよね。（自嘲）

れもん

まぁでも、このやり方が広まれば、データの分析を解ける受験生が増えますから、その人たちにがんばってもらいましょうよ。

キャタピラー表を時計回りに動かす。

Lukia

さて、正しい平均値が$ \ 24 \ $とわかり、仮平均の$ \ 25 \ $との差が$ \ 1 \ $あるので、時計回りに1動かします。

仮平均

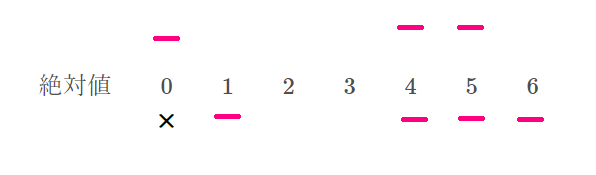
正しい平均

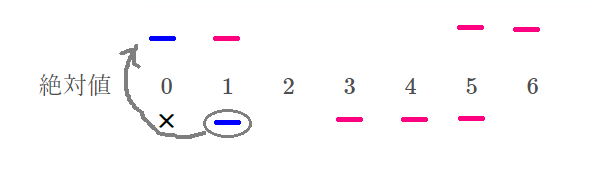
Lukia

二つの図を見比べてほしいのですが、
仮平均では$ \ -1 \ $だった$ \ 24 \ $が$ \ 1 \ $つ繰り上がって、$ \ 0 \ $になります。
動くのは、$ \ 24 \ $だけでなく、他のデータもそれぞれ一つずつ繰り上がるわけですから、
絶対値の下の値は、左にひとつずれ、
絶対値の上の値は、右にひとつずれます。

れもん

なるほど～！

Lukia

今回は、仮平均に比べて正しい平均の方が値が小さかったので、時計回りにずれましたが、
仮平均に比べて正しい平均の値が大きい場合は、反時計回りにずらせばいいですね。

Lukia

また、説明だけでは理解しにくいでしょうから、
また例題があるときに詳しくやりたいと思いますが、
絶対値の大きい方は、横に伸びると思ってください。絶対、上の値を下におろしたり、下の値を上にあげたりしちゃいけませんよ。

れもん

たとえばどういうことですか？

Lukia

今回のデータにもし$ \ 31 \ $が含まれていたとします。
仮平均との差は$ \ 6 \ $なので、絶対値$ \ 6 \ $の上に一書いてあるはずですね。
しかし、正しい平均が24ですから、

れもん

あ！差は$ \ +7 \ $であって、$ \ -6 \ $じゃない！

Lukia

おわかりいただけましたか？
だから、新たに絶対値$ \ 7 \ $を書き、その上に一を書くことになるんですね。

れもん

なるほど～！
絶対値が大きいほうの扱いさえ気を付ければ、簡単ですね！

キャタピラー表を用いれば偏差の二乗の和も簡単。

Lukia

偏差の二乗の和というのは、
$$\sum_{i=1}^{7}{\left( x_i-\overline{x}\right)^2}$$
のことです。
特に$ \ x_i \ $は、それぞれのデータのことを指し、
$ \ i \ $は、7人に連番を割り振ったようなものです。
$ \ \overline{x} \ $は、平均の値のことですね。

Lukia

キャタピラー表は、平均との絶対値で表されていますから、
真ん中の絶対値を2乗して、その絶対値に位置する人数をかけて、合計すればいいだけなんです。

$$\begin{align}\sum_{i=1}^{7}{\left( x_i-\overline{x}\right)^2}=&0^2\times 1+1^2\times 1+3^2\times 1+4^2\times 1+5^2\times 2+6^2\times 1 \ =&1+9+16+50+36 \ =&112 \end{align}$$