Yahoo!知恵袋の高校数学カテゴリにあった三角不等式を解いてみる。

2018年9月22日2023年1月15日三角関数実用数学技能検定（数学検定 数検),数検2級

[mathjax]

解法

$$\begin{align}左辺=&2\cos^{2} \theta-1+\sin \theta -1 \\\\ =&1-2\sin^{2} \theta+\sin \theta-1 \\\\ =&-2\sin^{2} \theta+\sin \theta \end{align}$$

Lukia

すなわち、新たに書き直せば、以下のような不等式になりますね。

$$\begin{align}-2\sin^{2} \theta+\sin \theta& \geq 0 　\\\\ただし、\left( 0 \leq \theta \leq \pi\right) \\\\ 2\sin^{2} \theta-\sin \theta& \leq 0 \\\\ \sin \theta\left( 2\sin \theta-1\right)& \leq 0\\\\ 0 \leq \sin \theta \leq \frac{1}{2} \end{align}$$

Lukia

「サインはV」ならぬ、「サインは\( y\)」で覚えましょう。

「サインはワイ」について、ちょっと脱線。

Lukia

\(xy\)平面上に、原点を中心とした半径1の円を描きます。
式としては、\(x^2+y^2=1\) ですね。

Lukia

その円周上のある点の座標を \(\mathrm{P}\left( x , y\right)\) とし、
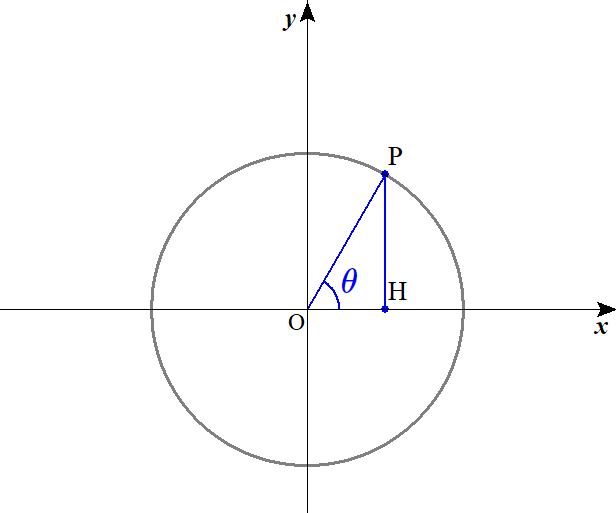
点\(\mathrm{P}\)からおろした垂線と\(x\)軸との交点を\(\mathrm{H}\left( x , 0\right)\)とします。
さらに、線分\(\mathrm{OP}\)と\(x\)軸とのなす角を\(\theta\)とします。

Lukia

三角形\(\mathrm{POH}\)において、
\(\sin \theta=\frac{\mathrm{PH}}{\mathrm{PO}}=\frac{y}{1}\) と表わせます。

Lukia

ということは、変形すれば、
\(y=\sin \theta\) とできますね。

Lukia

同様に、\(\cos \theta=\frac{\mathrm{OH}}{\mathrm{PO}}=\frac{x}{1}\) より、
\(x=\cos \theta\)となります。

いやいや、「サインはV」ってナニ？

「サインはV」とは、1960年代末ごろに人気のあった漫画、ドラマのタイトルで、
「スポーツ根性」略してスポ根こんドラマの草分け的存在なんだそうです。

さすがに、私も生まれてないので、ドラマや漫画を見たりしたことはないのですが、
高校1年生のときの数学の先生がしきりに、「サインはワイ」とおっしゃって印象付けてくれたので、
いまだに覚えています。

本線に戻ります。

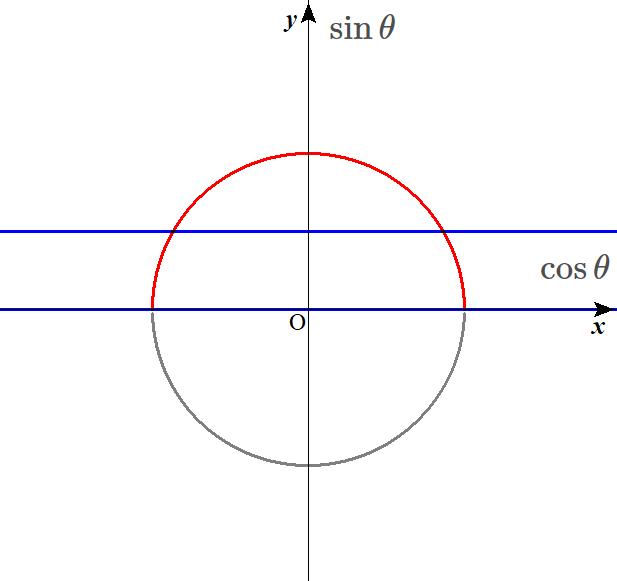
$$0 \leq \theta \leq \pi のときの、0 \leq \sin \theta \leq \frac{1}{2}　を求めます。$$

Lukia

\(0 \leq \theta \leq \pi\)は、上の図だと、赤い半円上の点と原点とを結んだ線分で表されます。

Lukia

また、\(0 \leq \sin \theta \leq \frac{1}{2}\)　は、
\(0 \leq y \leq \frac{1}{2}\) と置き換えてもさしつかえないのでしたから、
上の図の青い2本の直線に囲まれた部分に存在するといえます。

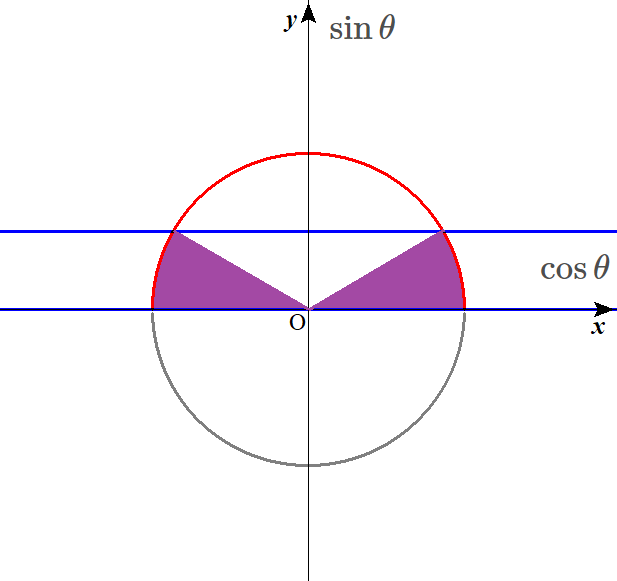
Lukia

そして、赤と青が重なるのが紫の部分です。
こたえるのは、角度\(\left( \theta\right)\)ですから、

$$ ゆえに、0 \leq \theta \leq \frac{ \pi }{ 6 }　 ,　 {\frac{ 5 }{ 6 }}\pi \leq \theta \leq \pi$$

こたえ

$$ 0 \leq \theta \leq \frac{ \pi }{ 6 }　 ,　 {\frac{ 5 }{ 6 }}\pi \leq \theta \leq \pi$$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。