高校数学の「分数不等式」に関する問題を解いてみる。（Yahoo!知恵袋より）

2019年1月21日2023年1月14日関数と極限実用数学技能検定（数学検定 数検),数検準1級

分子をシンプルに。

Lukia

今は、小学校の算数でいう仮分数のような状態です。
（\( \ \frac{8}{3} \ \)のような）
これを帯分数のような状態にします。（\( \ 2\frac{2}{3} \ \)のような）
分母で分子を割り、分子にはこれ以上割れない余りがのっているだけの状態にします。

$$\begin{align}\frac{x^2-2x}{x+1}=&\frac{x\left( x+1\right)-3x}{x+1} \\\\ =&x-\frac{3\left( x+1\right)-3}{x+1} \\\\ =&x-3+\frac{3}{x+1} \end{align}$$

Lukia

変形したことによって、直線の式と、双曲線の式になりました。
直線の式のほうを移項して、不等式にします。

$$\begin{align}与式=x-3+\frac{3}{x+1} \gt &0 \\\\ \frac{3}{x+1} \gt &-x+3 \end{align}$$

Lukia

双曲線は、漸近線が\( \ x=-1 \ , \ y=0 \ \)にあり、漸近線を軸とすると、第1象限と第3象限を通る曲線です。
これが、直線\( \ y=-x+3 \ \)よりも上にあるのはいつか。ということが問われているとわかりますね。

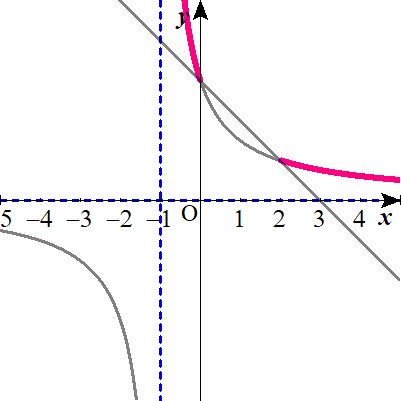
グラフより
$$-1 \lt x \lt 0 \ , \ 2 \lt x$$

こたえ

$$-1 \lt x \lt 0 \ , \ 2 \lt x$$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。