2019年大学入試センター試験数学1A「第4問不定方程式」を解いてみる。

2019年1月31日2023年1月14日大学入試センター試験,整数の性質実用数学技能検定（数学検定数検),数検2級,数検準2級

読了時間: 約9分15秒

[mathjax]

Lukia

はじめにおことわりを。
第4問は4つの小問からできていますが、この記事では、(1)と(2)について書くこととします。

小問1

問題

不定方程式　$ \ 49x-23y=1 \ $　の解となる自然数$ \ x \ , \ y \ $の中で,
$ \ x \ $の値が最小のものは
$ \ x=\color{#0004fc}{ア}\quad ,\quad y=\color{#0004fc}{イウ} \ $　であり,
すべての整数解は,$ \ k \ $を整数として
$ \ x=\color{#0004fc}{エオ}k+\color{#0004fc}{ア}\quad ,\quad y=\color{#0004fc}{カキ}k+\color{#0004fc}{いう} \ $　と表せる。

そもそも不定方程式を解くのが苦手な方のために。（読み飛ばしOK）

Lukia

不定方程式の解き方は人それぞれですね。
私は、アメーバブログで数学に関する記事を書いていらっしゃる方（お名前などは失念）のやり方を踏襲させていただいています。
YouTubeには、芸人のタカタ先生という方が不定方程式の解き方をレクチャーしていらっしゃいますが、形は違えど、やっていることは同じです。
いくつか動画やブログなどを見比べて、自分がやりやすい方法を覚えてください。

Lukia

まずは、単純に49と23の大きさを比べます。
すると、49の方が大きいですね。
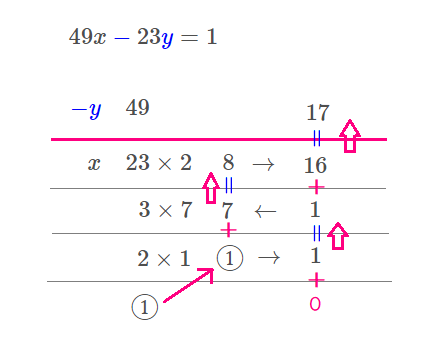
口の中でもごもご、式を言いながら、たすき掛けをするように数字や文字を配置します。
今回、$ \ y \ $の係数が$ \ -23 \ $となっていますので、
たすき掛けの際は、$ \ \Large \color{#0004fc}{-y} \ $と$ \ \LARGE 23 \ $に分けて書いてください。

Lukia

横書きだった$ \ 49x-23y \ $が縦書きになりました。
通常は、波線なのですが、パソコンでうまく書けなかったので、ピンク色の線としています。
これから、割り算をして下まで下がり、その後かけ算をしながら上に上がっていきます。このピンク色の線を超える数字が出たら完了です。

Lukia

$ \ 49\div23=2 \ 余り \ 3 \ $ですね。
商の2を23の右横に書いて$ \ \times \ $の記号でつないでおき、
余りの$ \ 3 \ $は、$ \ 23 \ $の下に書きます。

Lukia

次は、$ \ 23\div3=7 \ 余り \ 2 \ $ですね。
先ほどと同様に、
商の7を3の右横に書いて$ \ \times \ $の記号でつないでおき、
余りの$ \ 2 \ $は、$ \ 3 \ $の下に書きます。

Lukia

パターンがわかってきたと思いますが、
$ \ 3\div2=1 \ 余り \ 1 \ $です。
商の1を2の右横に書いて$ \ \times \ $の記号でつないでおき、
余りの$ \ 1 \ $は、$ \ 2 \ $の下に書きます。

Lukia

最後に出た余りの$ \ 1 \ $は、①などとしておくと、商の1と区別がついて、わかりやすいのでオススメです。
ひたすら①が出るまでこの操作を繰り返してください。

Lukia

それでは、いよいよピンク色の線を目指して、上に上がっていきます。
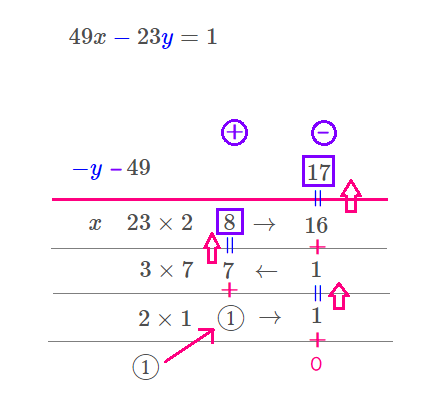
まずは、①を斜め右上にそのまま繰り上げます。
次に、左にある$ \ \times 1 \ $と文字通りかけ算し、答えを右向き矢印の方向に書きます。
$ \ ①\times 1=1 \ $となりますね。

Lukia

かけ算によってできた$ \ 1 \ $はもう一段上に上がるのですが、
一段上がるときには、一段下の数字とのたし算をして上がります。

Lukia

アメーバブログの方は、「ここはそのまま繰り上げます。」と説明していらっしゃったように記憶していますが、ほかの部分のやり方と統一するために、割り算によって求めた①の段の右横に$ \ \color{#f700ca}{0} \ $を書いておきましょう。
そうすれば、$ \ 1\left( かけ算の結果\right)\color{#f700ca}{+}\color{#f700ca}{0}\left( 一段下の数字\right)\color{#0004fc}{=}\left( 上向き矢印\right)1 \ $
と理解できますね。
しつこいようですが、下に図を貼っておきますので、確認してみてください。

Lukia

繰り上がった1と同じ段の左に書いてある$ \ \times 7 \ $でかけ算をし、こたえを左矢印の指す位置に書きます。
そして、「一段下の数字とたし算をして繰り上がる」のですから、
$ \ ①\color{#f700ca}{+}7\color{#0004fc}{=}8 \ $となりますね。

Lukia

ピンクの線を超えるまであともうひと息ですね。
$ \ 8\times 2=16 \ $で求めた$ \ 16 \ $を右矢印の指す位置に書き込みます。
そして、「一段下の数字とたし算をして繰り上がる」のですから、
$ \ 1\color{#f700ca}{+}16\color{#0004fc}{=}17 \ $　となり、
晴れて$ \ 17 \ $がピンクの線を超えましたので、操作完了です。

小問1を解く。

Lukia

先ほどの図に、紫の記号や、囲みを付け加えています。
この解き方のいいところは、紫の記号や囲みを使えば整数解や$ \ x \ , \ y \ $がぱっとわかることです。

$$x=\color{#0004fc}{8}\quad ,\quad y=\color{#0004fc}{17}$$

$$\begin{align}x&=\color{#0004fc}{23}k+\color{#0004fc}{8}\\\\ \color{#0004fc}{-y}=&\color{#740074}{-}49k\color{#740074}{-}17\ y\\\\&=\color{#0004fc}{49}k+\color{#0004fc}{17}\end{align}$$

小問2を解く。

問題

$ \ 49 \ $の倍数である自然数$ \ \mathrm{A} \ $と$ \ 23 \ $の倍数である自然数$ \ \mathrm{B} \ $の組$ \ \left( \mathrm{A}\quad ,\quad \mathrm{B}\right) \ $を考える。
$ \ \mathrm{A} \ $と$ \ \mathrm{B} \ $の差の絶対値が$ \ 1 \ $となる組$ \ \left( \mathrm{A}\quad ,\quad \mathrm{B}\right) \ $の中で,$ \ \mathrm{A} \ $が最小になるのは
$ \ \left( \mathrm{A}\quad ,\quad \mathrm{B}\right) \ = \ \left( 49\times \color{#0004fc}{ク}\quad ,\quad 23\times \color{#0004fc}{ケコ}\right) \ $　である。

$$\begin{align}\mathrm{A}=49x \ , \ \mathrm{B}=23y\quad &\left( x \ , \ y \ は自然数\right) \quad とする.\\\\ \vert \mathrm{A}-\mathrm{B} \vert=&1 \\\\ \vert 49x-23y \vert=&1\\\\ 49x-23y=&\color{#0004fc}{ \pm }1 \end{align}$$

Lukia

ぱっと見、(1)が使えそうですね。
それもあって$ \ \mathrm{A} \ $や$ \ \mathrm{B} \ $を$ \ 49x \ , \ 23y \ $とおいたわけですが、
二次試験レベルだと、おそらく$ \ x \ , \ y \ $が自然数である。ということをことわっておく必要があると思います。
ちなみに、なぜ「整数（自然数だけでなく、負も0もありうる）」ではなく、「自然数」と限定できたか。というと、
「$ \ \mathrm{A} \ $や$ \ \mathrm{B} \ $が自然数」とあるからです。
もし、$ \ x \ $や$ \ y \ $が負の整数や0だったら、自然数になりえませんからね。

Lukia

「自然数$ \ \mathrm{A} \ $が最小になる」ということは、
「自然数$ \ x \ $が最小になる」ということです。
そこで、$ \ 49x-23y= \pm 1 \ $を計算して求めた
$ \ \color{#0004fc}{x=23k+8}\quad \cdots\cdots\quad ① \ $と
$ \ \color{#f700ca}{x=23k-8}\quad \cdots\cdots\quad ② \ $のグラフを描いて考えてみたいと思います。
ちなみに、$ \ k \ $は整数です。

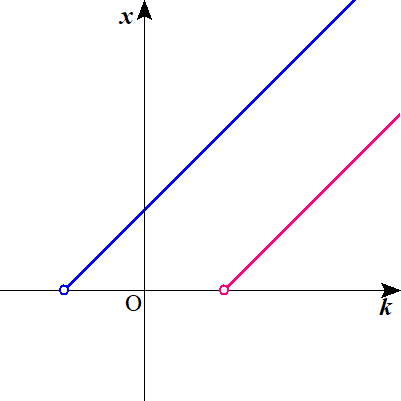
Lukia

実際の直線① , ②はもっと急激な右上がりなのですが、
正確なグラフが必要なわけではないので、デフォルメしています。

Lukia

2本の直線は、$ \ x \gt 0 \ $となるところから表しています。
青い線とピンクの線で見比べると、青い線の方が、$ \ k \ $の値が小さいうちから少なくとも正の数になるとわかりますね。
ピンクの線が正の数になるころには、青い線はだいぶ上をいっています。
つまり、整数$ \ k \ $が小さくても$ \ x \ $が自然数になりえるほうが、$ \ \mathrm{A} \ $に課せられた条件を満たす可能性がありますね。

Lukia

センター試験のときは、$ \ x \ $についての式を二つ作れたら、
単純に$ \ k=0 \ $を入れてみてください。時間がないので、それで判断しても十分だと思います。

$$\begin{align}x=&23k+8 \gt 0\quad となるのは, \\\\ -\frac{8}{23} \lt &k\quad のとき. \\\\ 条件を満たす整数 \ k \ は&k=0\\\\ ゆえに\quad &x=8\\\\ &y=49\cdot 0+17=17 \\\\ \left( \mathrm{A}\quad ,\quad \mathrm{B}\right) \ =& \ \left( 49\times \color{#0004fc}{8}\quad ,\quad 23\times \color{#0004fc}{17}\right) \end{align}$$

問題

また,$ \ \mathrm{A} \ $と$ \ \mathrm{B} \ $の差の絶対値が$ \ 2 \ $となる組$ \ \left( \mathrm{A}\quad ,\quad \mathrm{B}\right) \ $の中で,$ \ \mathrm{A} \ $が最小になるのは
$ \ \left( \mathrm{A}\quad ,\quad \mathrm{B}\right)=\left( 49\times \color{#0004fc}{サ}\quad ,\quad 23\times \color{#0004fc}{シス}\right) \ $　である。

$$\begin{align}\vert \mathrm{A}-\mathrm{B} \vert=&2 \\\\\ \vert 49x-23y\vert=&2 \\\\ 49x-23y=& \pm 2 \end{align}$$
$$\left( 以下, \ k \ は整数とする.\right)$$
$$\begin{align}ⅰ\quad &\quad 49x-23y=2\quad のとき \\\\ &\quad \quad x=23k+16 \\\\ &\quad \quad y=49k+34 \end{align}$$

$$\begin{align}ⅱ\quad &\quad 49x-23y=-2\quad のとき \\\\ &\quad \quad x=23k-16=23k+\left( 23-16\right)=23k+7 \\\\ &\quad \quad y=49k-34=49k+\left( 49-34\right)=49k+15 \end{align}$$
$$\begin{align}ⅰ \ , \ ⅱ \ より&自然数 \ \mathrm{A} \ が最小になる自然数 \ x \ の値は \\\\ x=&7\quad ,\quad y=15 \\\\ 以上より&\left( \mathrm{A}\quad ,\quad \mathrm{B}\right)=\left( 49\times \color{#0004fc}{7}\quad ,\quad 23\times \color{#0004fc}{15}\right) \end{align}$$

Lukia

小問2の絶対値がらみの部分がややこしいですね。
前半は(1)の勢いでなんとなくできそうですが、
後半は、　$ \ \vert 49x-23y \vert=2 \ $を
いかに早く$ \ 49x-23y=\color{#0004fc}{ \pm }2 \ $に読み替えられるかにかかっていると思います。
頭の中の引き出しがいかにスムーズに開くか、どれだけ関連づけられているかが試されています。

Lukia

ふだんはわかっている問題でも、焦りや不安などで度忘れしてしまうこともあります。センター数学は、平常心が試されているのかもしれませんね。

2019年大学入試センター試験の数学の問題の一覧です。