高校数学の「3種の硬貨で1万円を表現する」問題を解いてみる。【Yahoo!知恵袋より】
Yahoo!知恵袋の高校数学カテゴリに掲載されていた「3種の硬貨で1万円を表現する」問題を解いてみました。
解法
100円硬貨の枚数を\( \ x \ \)枚とし、
10円硬貨の枚数を\( \ 10y \ \)枚とする。
500円硬貨の枚数は、\( \ \left( 100-10y-x\right) \ \)枚と表せる。
また、3種の硬貨の枚数の合計が100であることから、
\( \ 1 \leqq y \leqq 9\quad \cdots \ \rm{①} \ \)
さらに、100円硬貨の枚数は、10円硬貨の枚数よりも少ないことから、
\( \ 10y \gt x\quad \cdots \ \rm{②} \ \)を満たす必要がある。
3種の硬貨を用いて1万円を表す。
$$\begin{align}100x+500\left( 100-10y-x\right)=&10000-10\times 10y \\\\ 100x+50000-5000y-500x=&10000-100y \\\\ 両辺を&100で割って\\\\ x+500-50y-5x=&100-y\\\\ -4x-49y=&-400\\\\ 4x+49y=&400 \end{align}$$
一次不定方程式を解く。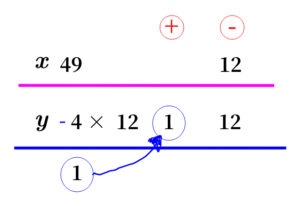
\( \ \begin{eqnarray} \left\{ \begin{array}{l} x = 49k-4800 \\ y = -4k+400 \end{array} \right. \end{eqnarray} \ \) （ただし、\( \ k \ \) は整数.）
①より
$$\begin{align}1 \leqq &-4k+400 \leqq 9 \\\\ -391 \leqq &-4k \leqq -391 \\\\ 97.75 \leqq &k \leqq 99.75\quad \cdots \ \rm{③} \end{align}$$ ②より
$$\begin{align}10\left( -4k+400\right) \gt &49k-4800 \\\\ -40k+4000 \gt &49k-4800 \\\\ 8800 \gt &89k\\\\ 98.88 \gt &k\quad \cdots\cdots \ ④ \end{align}$$ ③と④より
\( \ 99.75 \lt k \lt 98.89 \ \) を満たす整数 \( \ k \ \) は
$$\begin{align}x=&49\times 98-4800 \\\\ =&2 \end{align}$$
検算してみる
\( \ k=98 \ \)のとき、\( \ x=2 \ \) , \( \ y=8 \ \)となります。$$\begin{align}\rm{与式}=&10\times 10y+100\times x+500\times \left( 100-10y-x\right)\\\\ =&10\times \left( 10\times 8\right)+100\times 2+500\times \left( 100-10\times 8-2\right) \\\\ =&10\times 80+100\times 2+500\times 18 \\\\ =&800+200+9000\\\\ =&10000 \end{align}$$
こたえ
\( \ 2 \ \)枚
共有:
プロフィール
