高校数学の「絶対値がらみの放物線と動く定義域」に関する問題を解いてみる。【Yahoo!知恵袋より】
Yahoo!知恵袋の高校数学カテゴリに掲載されていた「絶対値がらみの放物線と動く定義域」に関する問題を解いてみました。
解法
\( \ y=f\left( x\right) \ \) とする。
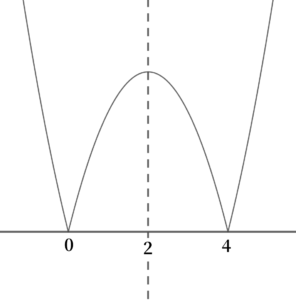
曲線\( \ f\left( x\right)=\vert x^2-4x \vert \ \)のグラフは以下の図のとおり。
 |
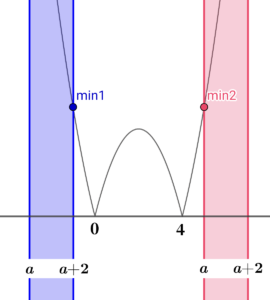① \( \ a+2 \lt 0 \ \) すなわち、\( \ a \lt -2 \ \) のとき 定義域は、左図の青い範囲 最小値は、\( \ f\left( a+2\right)=a^2-4 \ \) |
| ② \( \ 4 \lt a \ \) のとき 定義域は、左図の赤い範囲 最小値は、\( \ f\left( a\right)=a^2-4a \ \) |
|
 |
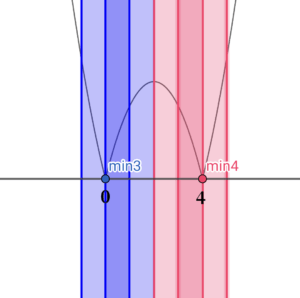③ \( \ -2 \leqq a \leqq 0 \ \) のとき、 定義域は、左図の青い範囲 最小値は、\( \ f\left( 0\right)=0 \ \) |
| ④ \( \ 2 \leqq a \leqq 4 \ \) のとき、 定義域は、左図の赤い範囲 最小値は、\( \ f\left( 4\right)=0 \ \) |
|
 定義域が薄い青（または赤）と濃い青（または赤）に塗りつぶされていますが、
左端が右に1移動すると、右端も同様に右に1移動することを表しています。 しかし、その定義域には、かならず\( \ x=0 \ \)(青い定義域の場合）または、\( \ x=4 \ \)(赤い定義域の場合）が含まれていますので、最小値は\( \ f\left( 0\right)=0 \ \) または \( \ f\left( 4\right)=0 \ \)になるのです。 |
|
 |
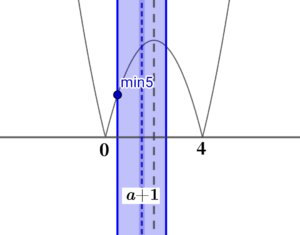⑤ \( \ 0 \lt a \lt 1 \ \) のとき、 定義域は、左図の青い範囲 最小値は、\( \ f\left( a\right)=-a^2+4a \ \) |
 |
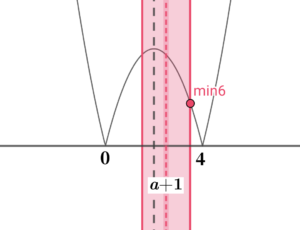⑥ \( \ 1 \lt a \lt 2 \ \) のとき、 定義域は、左図の赤い範囲 最小値は、\( \ f\left( a+2\right)=-a^2+4 \ \) |
|
⑤と⑥については、定義域の中間である\( \ x=a+1 \ \)と軸との位置関係を意識します。
軸から離れている端点のほうが最小値になっていますね。 |
|
 |
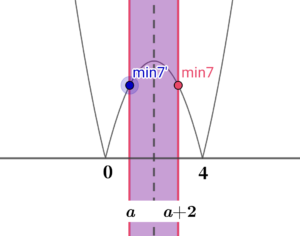⑦ \( \ a+1=2 \ \) すなわち、\( \ a=1 \ \) のとき 最小値は、\( \ f\left( 1\right)=f\left( 3\right)=3 \ \) |
|
定義域の中間である\( \ x=a+1 \ \)が、軸とぴったり重なったとき、定義域の両端点が最小値となります。
|
|
以上より最小値は
\begin{eqnarray} \left\{ \begin{array}{l} a^2-4&\quad a \lt -2\quad \rm{のとき} \\ 0&\quad -2 \leqq a \leqq 0 \ , \ 2 \leqq a \leqq 4\quad \rm{のとき}\\-a^2+4a& \quad 0 \lt a \lt 1\quad \rm{のとき}\\3&\quad a=1\quad \rm{のとき}\\-a^2+4&\quad 1 \lt a \lt 2\quad \rm{のとき}\\a^2-4a&\quad 4 \lt a\quad \rm{のとき} \end{array} \right. \end{eqnarray}
こたえ
\begin{eqnarray} \left\{ \begin{array}{l} a^2-4&\quad a \lt -2\quad \rm{のとき} \\ 0&\quad -2 \leqq a \leqq 0 \ , \ 2 \leqq a \leqq 4\quad \rm{のとき}\\-a^2+4a& \quad 0 \lt a \lt 1\quad \rm{のとき}\\3&\quad a=1\quad \rm{のとき}\\-a^2+4&\quad 1 \lt a \lt 2\quad \rm{のとき}\\a^2-4a&\quad 4 \lt a\quad \rm{のとき} \end{array} \right. \end{eqnarray}
共有:
プロフィール