高校数学の「放物線を平行移動させる」問題を解いてみる。【Yahoo!知恵袋より】

2022年9月8日2023年1月8日二次関数

Lukia

放物線の平行移動の問題は、頂点の座標を意識しましょう。

解法

平行移動後の放物線の頂点の座標を\( \ \left( \alpha \ , \ \ \beta\right) \ \) とする。
平行移動後の放物線は、\( \ y=-2\left( x-\alpha\right)^2+\beta \ \) と表せる。
頂点が放物線\( \ y=x^2+4 \ \)上にあるので、\( \ \beta=\alpha^2+4 \ \)と表せる。
\( \ y=-2\left( x-\alpha\right)^2+\alpha^2+4 \ \)は、 点 (\( \ 1 \ \),\( \ -3 \ \))を通るので、
$$\begin{align}-3=&-2\left( 1-\alpha\right)^2+\alpha^2+4 \\\\ -3=&-2\left( \alpha^2-2\alpha+1\right)+\alpha^2+4 \\\\ &-\alpha^2+4\alpha+5=0\\\\ &\left( -\alpha+5\right)\left( \alpha+1\right)=0\\\\ \alpha=&5 \ , \ -1 \end{align}$$ \begin{eqnarray} \left\{ \begin{array}{l} \alpha = 5 \\ \beta = 29 \end{array} \right. \end{eqnarray} \begin{eqnarray} \left\{ \begin{array}{l} \alpha = -1 \\ \beta = 5 \end{array} \right. \end{eqnarray}
ゆえに求める放物線の式は、
\( \ y=-2\left( x-5\right)^2+29 \ \)
\( \ y=-2\left( x+1\right)^2+5 \ \) である。（下の図の緑色の放物線）

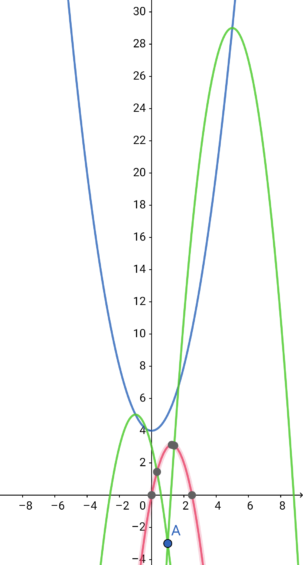
こたえ

\( \ y=-2\left( x-5\right)^2+29 \ \)
\( \ y=-2\left( x+1\right)^2+5 \ \)

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。