高校数学の「ユークリッドの互除法」に関する問題を解いてみる。（Yahoo!知恵袋より）

2019年4月5日2023年1月14日整数の性質実用数学技能検定（数学検定 数検),数検2級,数検準2級

[mathjax]

$$3x+4y=68\quad \left( x \gt 0 \ , \ y \gt 0\right)$$

Lukia

この問題を解くにあたってのポイントは、
「二つの数\( \ x \ , \ y \ \)が自然数である」という条件を
\( \ x \gt 0\quad ,\quad y \gt 0 \ \)と数学語に変換できるかどうかということですね。

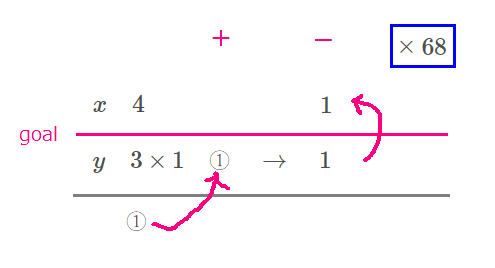
$$\begin{align}x=&\quad 4k\color{#f700ca}{-}\color{#0004fc}{68} \\\\ y=&-3k\color{#f700ca}{+}\color{#0004fc}{68} \quad \left( kは整数\right)\end{align}$$

Lukia

下書きでは、（\( \ k \ \)は実数）としていたのですが、
\( \ x \ \)や\( \ y \ \)が自然数（正の整数）であるためには、\( \ k \ \)は整数である必要があるので、さらに限定した表現の（\( \ k \ \)は整数）としました。

$$\begin{align}x \ と \ y \ がと&もに自然数であるための整数 \ k \ を求める.\\\\ x=&4k-68 \gt 0\quad を解いて, \ k& \gt 17\quad \cdots\cdots①\\\\ y=&-3k+68 \gt 0\quad を解いて,\\\\ k& \lt 22+\frac{2}{3}\quad \cdots\cdots②\\\\ ① \ , \ ② \ より&\quad 17 \lt k \lt 22+\frac{2}{3} \\\\ ゆえに求める整数 \ k \ は,&\quad k=18 \ , \ 19 \ , \ 20 \ , \ 21 \ , \ 22 \end{align}$$
$$\begin{align}さらに, \ 自然数 \ x \ &が2桁であるためには, \\\\ x=&4k-68 \geq 10\quad を満たす必要がある. \\\\ これを解いて,&\quad k \geq 19+\frac{1}{2}\\\\ すなわち,&k=20\quad のとき,条件を満たす.\\\\ 以上より,&求める自然数の組は,\\\\ x=&4\times 20-68=12\\\\ y=&-3\times 20+68=8\\\\ \left( x \ , \ y\right)=&\left( 12 \ , \ 8\right) \end{align}$$

こたえ

$$ \left( x \ , \ y\right)=\left( 12 \ , \ 8\right) $$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。