【 12 / 12 】高校数学の「平面ベクトルの点Pの存在範囲」に関する問題を解いてみる。

読了時間: 約3分25秒
[mathjax]問題
\( \ \triangle \mathrm{OAB} \ \)が、
\( \ \vert \mathrm{OA} \vert=5 \ \) , \( \ \vert \mathrm{OB} \vert=6 \ \) , \( \ \vert \mathrm{AB} \vert=7 \ \) を満たす三角形であり、
点\( \ \mathrm{P} \ \)が
\( \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}} \ \)
と \( \ s \geq 0 \ , \ t \geq 0 \ , \ 1 \leq 2s+t \leq 2 \ , \ s+3t \leq 3 \ \)を満たしながら動くとき、
点\( \ \mathrm{P} \ \)の存在範囲の面積を求めよ。
( ただし\( \ s \ \) , \( \ t \ \) はともに実数とする )
\( \ \vert \mathrm{OA} \vert=5 \ \) , \( \ \vert \mathrm{OB} \vert=6 \ \) , \( \ \vert \mathrm{AB} \vert=7 \ \) を満たす三角形であり、
点\( \ \mathrm{P} \ \)が
\( \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}} \ \)
と \( \ s \geq 0 \ , \ t \geq 0 \ , \ 1 \leq 2s+t \leq 2 \ , \ s+3t \leq 3 \ \)を満たしながら動くとき、
点\( \ \mathrm{P} \ \)の存在範囲の面積を求めよ。
( ただし\( \ s \ \) , \( \ t \ \) はともに実数とする )
解法
まずは、\( \ st \ \)平面上で点Pの存在範囲を求めます。\( \ s \ \)と\( \ t \ \)の条件より
\( \ s \geq 0 \ \)
\( \ t \geq 0 \ \)
\( \ t \leq 2-2s \ \)
\( \ t \geq 1-2s \ \)
\( \ t \leq 1- \ \)\(\Large \frac{1}{3}s\)
求める領域は、図の赤斜線部(境界を含む)

この赤斜線部を四角形\( \ \mathrm{AQBR} \ \)とする。
点\( \ \mathrm{Q} \ \)は、\( \ \left( s \ , \ t\right)= \ \)\(\Large \left( \frac{3}{5} \ , \ \frac{4}{5}\right)\)
点\( \ \mathrm{R} \ \)は、\( \ \left( s \ , \ t\right)= \ \)\(\Large \left( \frac{1}{2} \ , \ 0\right)\)である。
三角形\( \ \mathrm{OA’B’} \ \)における四角形\( \ \mathrm{AQBR} \ \)の面積比を求める。

$$\begin{align}\triangle \mathrm{OAB’}=&\frac{1}{3}\triangle \mathrm{OA’B’} \\\\ \\\\ 四角形\mathrm{AQBR}=&\triangle \mathrm{OAB’}-\triangle \mathrm{BQB’}-\triangle \mathrm{ORB} \\\\ =&\frac{1}{2}\times 1\times 2-\frac{1}{2}\times 1\times \left( \frac{3}{5}+\frac{1}{2}\right)\\\\ =&\frac{9}{10}\triangle \mathrm{OAB’} \\\\ =&\frac{9}{10}\times \frac{1}{3}\triangle \mathrm{OA’B’}\\\\ =&\frac{3}{10}\triangle \mathrm{OA’B’} \end{align}$$
\( \ \triangle \mathrm{OAB} \ \)において\( \ \theta=\angle \mathrm{AOB} \ \)とする。

余弦定理より
$$\begin{align}\cos \theta=&\frac{5^2+6^2-7^2}{2\cdot 5\cdot 6} \\\\ =&\frac{1}{5} \\\\ \\\\ \sin \theta=&\sqrt{1-\cos^{2} \theta}\\\\ =&\frac{2\sqrt{6}}{5} \end{align}$$
\( \ \triangle \mathrm{OA’B’} \ \)の面積\( \ \mathrm{S} \ \)を求める
\( \ \vert \overrightarrow{\mathrm{OA’}} \vert=3\vert \overrightarrow{\mathrm{OA}} \vert=15 \ \),
\( \ \vert \overrightarrow{\mathrm{OB’}} \vert=2\vert \overrightarrow{\mathrm{OB}} \vert=12 \ \) より
$$\begin{align}\mathrm{S}=&\frac{1}{2}\cdot 15\cdot 12\cdot \frac{2\sqrt{6}}{5}\\\\ =&36\sqrt{6} \\\\ \\\\ 四角形\mathrm{AQBR}=&\frac{3}{10}\cdot 36\sqrt{6}\\\\ =&\frac{51\sqrt{6}}{5} \end{align}$$
\( \ s \geq 0 \ \)
\( \ t \geq 0 \ \)
\( \ t \leq 2-2s \ \)
\( \ t \geq 1-2s \ \)
\( \ t \leq 1- \ \)\(\Large \frac{1}{3}s\)
求める領域は、図の赤斜線部(境界を含む)
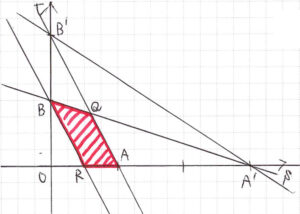
この赤斜線部を四角形\( \ \mathrm{AQBR} \ \)とする。
点\( \ \mathrm{Q} \ \)は、\( \ \left( s \ , \ t\right)= \ \)\(\Large \left( \frac{3}{5} \ , \ \frac{4}{5}\right)\)
点\( \ \mathrm{R} \ \)は、\( \ \left( s \ , \ t\right)= \ \)\(\Large \left( \frac{1}{2} \ , \ 0\right)\)である。
三角形\( \ \mathrm{OA’B’} \ \)における四角形\( \ \mathrm{AQBR} \ \)の面積比を求める。

$$\begin{align}\triangle \mathrm{OAB’}=&\frac{1}{3}\triangle \mathrm{OA’B’} \\\\ \\\\ 四角形\mathrm{AQBR}=&\triangle \mathrm{OAB’}-\triangle \mathrm{BQB’}-\triangle \mathrm{ORB} \\\\ =&\frac{1}{2}\times 1\times 2-\frac{1}{2}\times 1\times \left( \frac{3}{5}+\frac{1}{2}\right)\\\\ =&\frac{9}{10}\triangle \mathrm{OAB’} \\\\ =&\frac{9}{10}\times \frac{1}{3}\triangle \mathrm{OA’B’}\\\\ =&\frac{3}{10}\triangle \mathrm{OA’B’} \end{align}$$
\( \ \triangle \mathrm{OAB} \ \)において\( \ \theta=\angle \mathrm{AOB} \ \)とする。
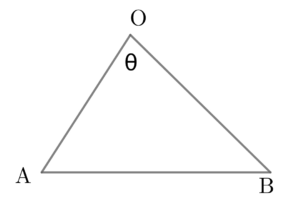
余弦定理より
$$\begin{align}\cos \theta=&\frac{5^2+6^2-7^2}{2\cdot 5\cdot 6} \\\\ =&\frac{1}{5} \\\\ \\\\ \sin \theta=&\sqrt{1-\cos^{2} \theta}\\\\ =&\frac{2\sqrt{6}}{5} \end{align}$$
\( \ \triangle \mathrm{OA’B’} \ \)の面積\( \ \mathrm{S} \ \)を求める
\( \ \vert \overrightarrow{\mathrm{OA’}} \vert=3\vert \overrightarrow{\mathrm{OA}} \vert=15 \ \),
\( \ \vert \overrightarrow{\mathrm{OB’}} \vert=2\vert \overrightarrow{\mathrm{OB}} \vert=12 \ \) より
$$\begin{align}\mathrm{S}=&\frac{1}{2}\cdot 15\cdot 12\cdot \frac{2\sqrt{6}}{5}\\\\ =&36\sqrt{6} \\\\ \\\\ 四角形\mathrm{AQBR}=&\frac{3}{10}\cdot 36\sqrt{6}\\\\ =&\frac{51\sqrt{6}}{5} \end{align}$$
こたえ
\(\Large \frac{51\sqrt{6}}{5} \)
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません