2019年大学入試センター試験 数学2B「第4問 ベクトル」を解いてみる。

2019年1月27日2023年1月14日ベクトル,大学入試センター試験実用数学技能検定（数学検定 数検),数検2級,数検準1級

[mathjax]

$$\begin{align}\overrightarrow{a}\cdot \overrightarrow{c}=0 \ より\quad \angle \mathrm{AOC}=&\color{#0004fc}{90}^{\circ} \\\\ 三角形 \ \mathrm{OAC} \ の面積を\mathrm{S}とする.\\\\ \mathrm{S}=\frac{1}{2}\mathrm{OA\cdot OC}=&\color{#0004fc}{\frac{\sqrt{5}}{2}}\end{align}$$

Lukia

ここからは、いよいよベクトルに関するさまざまな計算をしていくわけですが、ひとつ提案してみたいのが、「生物の遺伝」式かけ算です。（インド式計算ともいえるかな？）
センター試験で厄介な点は、計算スペースの確保です。
通常のベクトルの計算だと、どんどん横に長くなっていきますので、ほかのことに使おうとしても、消しゴムで計算を消したりしなければなりません。
生物の遺伝で、雌雄の遺伝子から子の遺伝子を考える問題がありますが、そこで用いるようなマスを描いて、一気にかけ算し、
そのあとゆっくりたし算をするという、「計算のバッチ化」を行えば、省スペースで、結果も確実となります。

$$\overrightarrow{\mathrm{BA}}\cdot \overrightarrow{\mathrm{BC}}=\color{#0004fc}{-1}$$

$$\vert \overrightarrow{\mathrm{BA}}\vert=\sqrt{\color{#0004fc}{2}}$$

$$\vert \overrightarrow{\mathrm{BC}}\vert=\sqrt{\color{#0004fc}{2}}$$

$$\begin{align}\cos \angle \mathrm{ABC}=&\frac{\overrightarrow{\mathrm{BA}}\cdot \overrightarrow{\mathrm{BC}}}{\vert \overrightarrow{\mathrm{BA}} \vert\vert \overrightarrow{\mathrm{BC}} \vert}=\frac{-1}{\sqrt{2}\cdot \sqrt{2}}=-\frac{1}{2}\quad より \\\\ \\\\ \angle \mathrm{ABC}=&\color{#0004fc}{120}^{\circ} \end{align}$$

$$\begin{align}四角形 \ \mathrm{ABCD} \ は\mathrm{AB}=&\mathrm{DC} \ の等脚台形. \\\\ \mathrm{AD}//\mathrm{BC} \ より\angle \mathrm{BAC}は\angle &\mathrm{CBA}の外角と錯角の関係にあるので, \\\\ \angle \mathrm{BAD}=\angle \mathrm{ADC}=&\color{#0004fc}{60}^{\circ} \end{align}$$

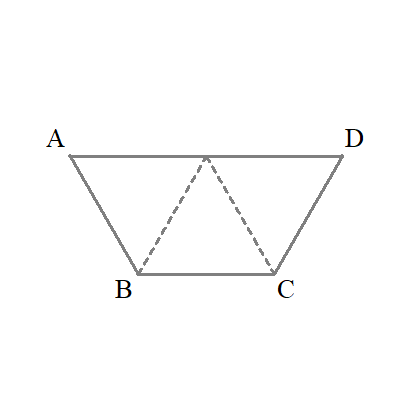
$$\begin{align}また, \ 四角形\mathrm{ABCD}は&一辺の長さ \ \sqrt{2} \ の正三角形が\\\\ 三つ合わさったものと&考えられるので, \\\\ \overrightarrow{\mathrm{AD}}=&\color{#0004fc}{2}\overrightarrow{\mathrm{BC}} \\\\ \mathrm{S_{ABCD}}=&3\times \frac{1}{2}\times \left( \sqrt{2}\right)^2\times \sin 60^{\circ}\\\\ =&\color{#0004fc}{\frac{3\sqrt{3}}{2}} \end{align}$$

条件より,
$$\overrightarrow{\mathrm{BH}}\cdot \vec{a}=\color{#0004fc}{0} \ , \ \overrightarrow{\mathrm{BH}}\cdot \vec{c}=0$$

$$\begin{align}\overrightarrow{\mathrm{BH}}=&\overrightarrow{\mathrm{OH}}-\vec{b} \\\\ =&s\vec{a}-\vec{b}+t\vec{c}\end{align}$$
$$\overrightarrow{\mathrm{BH}}\perp \vec{a} \ と \ \overrightarrow{\mathrm{BH}}\perp \vec{c} \ を計算する.$$

$$s=\color{#0004fc}{1} \ , \ t=\color{#0004fc}{\frac{3}{5}}$$

$$ゆえに, \ \overrightarrow{\mathrm{BH}}=\vec{a}-\vec{b}+\frac{3}{5}\vec{c} \ と表せる.$$

$$\begin{align}\vert \overrightarrow{\mathrm{BH}} \vert^2=&\frac{1}{5}\quad より \\\\ \vert \overrightarrow{\mathrm{BH}} \vert=&\color{#0004fc}{\frac{\sqrt{ネ}}{ノ}}\end{align}$$

$$\begin{align}\mathrm{V}=&\frac{1}{3}\mathrm{S}\cdot \vert \overrightarrow{\mathrm{BH}} \vert=\color{#0004fc}{\frac{1}{6}} \end{align}$$

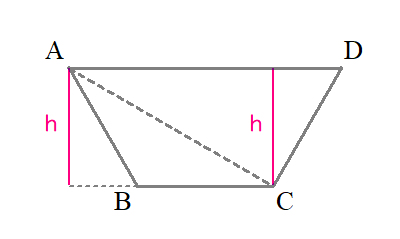
二つの三角形の面積比
$$\begin{align}\triangle \mathrm{ABC}:\triangle \mathrm{ACD}=&1:2 \ だから, \\\\ 四角錐\mathrm{OABCD}の体積は&\color{#0004fc}{3}\mathrm{V} \\\\ \\\\ ここで,求める高さを\quad &h \ とする.\\\\ 3\mathrm{V}=&\frac{1}{3}\times □\mathrm{ABCD}\times h\\\\ 3\cdot 3\cdot \frac{2}{3\sqrt{3}}\cdot \frac{1}{6}=&h\\\\ h=&\color{#0004fc}{\frac{\sqrt{3}}{3}} \end{align}$$

Lukia

はじめのうちは、四角形\( \ \mathrm{ABCD} \ \)の形がイメージできないかもしれません。
ほとんどの人は、平行四辺形か、等脚台形の可能性があることまでは導けるでしょうが、
一発で\( \ \mathrm{AD} \gt \mathrm{BC} \ \)の等脚台形を想定するのは難しいと思います。
ベクトルの問題を解くときは、基本、反時計回りに点をおく図形をうす～く描いておき、情報が得られるたびに描き直していくのがいいと思います。

Lukia

ちなみに、図形に点を打つときは、反時計回りで。というのは、
私の長年の経験から得られたものです。
当然、例外（時計回りで点を打つ図形）もあるのですが、これはかなり稀まれなパターンです。

2019年大学入試センター試験の数学の問題の一覧です。

2019年大学入試センター試験 数学1A 2Bの解答一覧

2019年1月20日に実施された大学入試センター試験の数学ⅠA , ⅡBの問題を解いてみました。 一覧表があっ ...

 https://makelemonadejp.com/center20191a2b/

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。