中学数学の食塩水「とりだし」問題(その2)

読了時間: 約3分0秒

Lukia
さぁ、前回に引き続き、
「とりだし」問題を解いていきましょう。
ヒントとして、

を載せておきますね。
本当に、「とりだし」問題なのかどうかを確認してから、解くようにしましょうね。
「とりだし」問題を解いていきましょう。
ヒントとして、
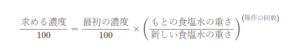
を載せておきますね。
本当に、「とりだし」問題なのかどうかを確認してから、解くようにしましょうね。
解法
あいうえお
こたえ
あいうえお
問題
10%の食塩水が100g入っている容器がある。
この容器から20gの食塩水を取り出してから、同じ量の水を加えてよくかき混ぜるという操作を3回繰り返すと、食塩水の濃度は何%になるか。
この容器から20gの食塩水を取り出してから、同じ量の水を加えてよくかき混ぜるという操作を3回繰り返すと、食塩水の濃度は何%になるか。
変わるもの、変わらないものを確認する。

もも
もともとの食塩水の濃度は、10%で、
その食塩水から20g取り出したのですから、
10%の食塩水は、80g残っていることになります。
その食塩水から20g取り出したのですから、
10%の食塩水は、80g残っていることになります。

Lukia
そうですね。

もも
そして、その10%食塩水80gに、20gの水を加えるのですから、
新たにできる食塩水は、濃度はぱっとわからないけど、
重さは、100gになるわけですね。
新たにできる食塩水は、濃度はぱっとわからないけど、
重さは、100gになるわけですね。

Lukia
そのとおりです。

もも
濃度はわからないけど、食塩水80gに、水20gを加える。という操作を3回繰り返すわけだから・・・

もも
これは、公式にあてはめてよさそうです!
公式にあてはめながら、式を立てる。

Lukia
そうですか。
では、公式を見ながら、式を立ててみてください。

では、公式を見ながら、式を立ててみてください。
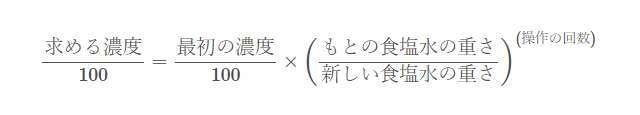

もも
はい。
「求める濃度」を \(\Large x\) とし、
「最初の濃度」は \(\Large 10\) 、
「もとの食塩水の重さ」は、 \(\Large 80\) 、
「新しい食塩水の重さ」は、 \(\Large 100\) 、
操作の回数は、 \(\Large 3\) だから・・・
「求める濃度」を \(\Large x\) とし、
「最初の濃度」は \(\Large 10\) 、
「もとの食塩水の重さ」は、 \(\Large 80\) 、
「新しい食塩水の重さ」は、 \(\Large 100\) 、
操作の回数は、 \(\Large 3\) だから・・・

もも
$$\Large \frac{x}{100}=\frac{10}{100}\times \left( \frac{80}{100}\right)^3$$となります。
計算して、こたえを求める。

Lukia
それでは、式を計算して、こたえをもとめていきましょう。
$$\Large \frac{x}{100}=\frac{10}{100}\times \left( \frac{80}{100}\right)^3$$
約分する。
$$\Large \frac{x}{100}=\frac{10}{100}\times \left( \frac{4}{5}\right)^3$$
両辺の分母の100をはらい、累乗をかけ算に直す。
$$\Large x=10\times \frac{4\times 4\times 4}{5\times 5\times 5}=\frac{2\times 4\times 4\times 4}{5\times 5}$$
分子・分母に4をかける。
$$\Large x=\frac{2\times 4\times 4\times 4}{5\times 5}\times \frac{4}{4}=\frac{2\times 4\times 4\times 4\times 4}{100}$$

Lukia
ここで、\(\Large 4=2^2\) であり、
\(\Large 2\times 4\times 4\times 4\times 4=2\times 2^2\times 2^2\times 2^2\times 2^2\) です。
\(\Large 2\times 4\times 4\times 4\times 4=2\times 2^2\times 2^2\times 2^2\times 2^2\) です。

Lukia
さらに、
\(\Large 2\times 2^2\times 2^2\times 2^2\times 2^2=2^\left( 1+2+2+2+2\right)=2^9\) です。
\(\Large 2\times 2^2\times 2^2\times 2^2\times 2^2=2^\left( 1+2+2+2+2\right)=2^9\) です。

Lukia
ここで、\(\Large 2^{10}=1024\) を変形させてこたえを求めます。
\(\Large 2^{10}=2^\left( 9+1\right)=2^9\times 2\) なので、
\(\Large 2^9=2^{10}\times \frac{1}{2}=1024\times \frac{1}{2}=512\) となります。
\(\Large 2^{10}=2^\left( 9+1\right)=2^9\times 2\) なので、
\(\Large 2^9=2^{10}\times \frac{1}{2}=1024\times \frac{1}{2}=512\) となります。
つまり、
$$\Large x=\frac{512}{100}=5.12$$

Lukia
最終的に食塩水の濃度は、5.12 %になります。
こたえ

Lukia
いかがでしたか。
「公式化」していなければ、表を3回描いて、3つ式をたて、計算していかなければなりませんでした。
それが、変わる部分、変わらない部部分をきっちり確認するだけで、短い式を一つ立て、
計算するだけで済むわけです。
「公式化」していなければ、表を3回描いて、3つ式をたて、計算していかなければなりませんでした。
それが、変わる部分、変わらない部部分をきっちり確認するだけで、短い式を一つ立て、
計算するだけで済むわけです。
5.12 %
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません