中学数学の食塩水に「水」を混ぜる問題(その1)

読了時間: 約3分26秒
[mathjax]

Lukia
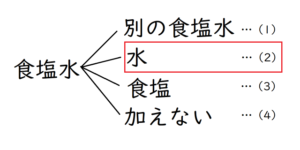
さて、今回からは、「食塩水に『水』を加える」問題を解いていきます。
食塩水に加えるものとしては、「別の濃度の食塩水」・「食塩水」・「水」とありましたが、
「水」がいよいよ最後のパターンとなります。

食塩水に加えるものとしては、「別の濃度の食塩水」・「食塩水」・「水」とありましたが、
「水」がいよいよ最後のパターンとなります。
問題
濃度12%の食塩水400gに水200gを加えると、濃度は何%になるか。
表に書き込む。

もも
まずは、いつもどおり、
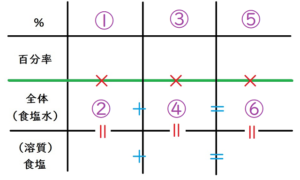
横長の線を3本描いて、その線を4等分できるように、縦に3本の線を引いていきます。
横長の線を3本描いて、その線を4等分できるように、縦に3本の線を引いていきます。

Lukia
ももちゃんは、以下のような表を描いています。

もも
そして、表に数字を書き込みます。
①が12、
②が400です。
①が12、
②が400です。

もも
③は・・・

Lukia
はい。
ここが「水」を加える問題のポイントですね。
ここが「水」を加える問題のポイントですね。

Lukia
ももちゃん、つかぬことをお聞きしますが、
「水」が100gあったとして、その「水」に「食塩」は何g含まれていますか?
「水」が100gあったとして、その「水」に「食塩」は何g含まれていますか?

もも
「水」に「食塩」?
いいえ、含まれていませんよ。
水道ひねって、塩水出てきたら問題アリじゃないですか。
いいえ、含まれていませんよ。
水道ひねって、塩水出てきたら問題アリじゃないですか。

Lukia
そ~ですよねぇ。
じゃ、変なはなし、「水」って、「何%食塩水」ですか?(笑)
じゃ、変なはなし、「水」って、「何%食塩水」ですか?(笑)

もも
0%食塩水ですッ!
あっ、③は0ってことですか?
あっ、③は0ってことですか?

Lukia
そうなんです。(笑)
「水」は、「0%食塩水」と考えれば、この表も簡単にうめていけるんですね。
「水」は、「0%食塩水」と考えれば、この表も簡単にうめていけるんですね。

もも
なるほど~。
じゃ、③は0 だ。
④は200 となりますね。
じゃ、③は0 だ。
④は200 となりますね。

もも
いつものように、
全体の重さの段は、「横にたし算」ができるから、
②+④=⑥ となるので、
⑥は、600 とわかります。
全体の重さの段は、「横にたし算」ができるから、
②+④=⑥ となるので、
⑥は、600 とわかります。

もも
ちょっと番号が前後してしまったけど、
今回はできあがる食塩水の濃度を求めるのだから、
⑤は \(\Large x\) となりますね。
今回はできあがる食塩水の濃度を求めるのだから、
⑤は \(\Large x\) となりますね。
%を百分率に直しておく。

もも
百分率に直すのは簡単です。
左から、
\(\Large \frac{12}{100}\) ・ \(\Large \frac{0}{100}\) ・ \(\Large \frac{x}{100}\) となります。
左から、
\(\Large \frac{12}{100}\) ・ \(\Large \frac{0}{100}\) ・ \(\Large \frac{x}{100}\) となります。
縦はかけ算・横はたし算

Lukia
それでは、「縦はかけ算」をして、表の一番下の段のマスをうめていってください。

もも
は~い。
まず、12%食塩水の列は、
\(\Large \frac{12}{100}\times 400\) となります。
まず、12%食塩水の列は、
\(\Large \frac{12}{100}\times 400\) となります。

もも
水、つまり0%食塩水の列は、
\(\Large \frac{0}{100}\times 200\) となります。
\(\Large \frac{0}{100}\times 200\) となります。

もも
えっ、でも、 \(\Large \frac{0}{100}=0\) で、
\(\Large 0\times 200=0\) となりますよ?
\(\Large 0\times 200=0\) となりますよ?

Lukia
はい。ですから、
一番下の段のマスには、0を書き込めばよいのです。
一番下の段は、それぞれの重さに含まれる「食塩の重さ」が書き込まれます。
「水」に「食塩」が含まれていないのですから、0なのはあたりまえといえますね。
一番下の段のマスには、0を書き込めばよいのです。
一番下の段は、それぞれの重さに含まれる「食塩の重さ」が書き込まれます。
「水」に「食塩」が含まれていないのですから、0なのはあたりまえといえますね。

Lukia
表を描いて、式を立てる人ならば、慣れてくれば
いきなり一番下の段に0を書き込んでもいいですよ。
(ただし、このシリーズでは、きっちり式を立てていきますけどね)
いきなり一番下の段に0を書き込んでもいいですよ。
(ただし、このシリーズでは、きっちり式を立てていきますけどね)

もも
わかりました。
では、できあがる食塩水の列へ。
\(\Large \frac{x}{100}\times 600\) となります。
では、できあがる食塩水の列へ。
\(\Large \frac{x}{100}\times 600\) となります。
一番下の段の「たし算」をする。

Lukia
それでは、表の一番下の段の「横はたし算」をして、式を立ててみてください。

もも
はい。
\(\Large \frac{12}{100}\times 400+0=\frac{x}{100}\times 600\) ですが、
0は書く必要がないので、
\(\Large \frac{12}{100}\times 400=\frac{x}{100}\times 600\) となります。
\(\Large \frac{12}{100}\times 400+0=\frac{x}{100}\times 600\) ですが、
0は書く必要がないので、
\(\Large \frac{12}{100}\times 400=\frac{x}{100}\times 600\) となります。

Lukia
はい。よくできました。計算は、ふきだしをはずしてやってみましょう。
$$\Large \frac{12}{100}\times 400=\frac{x}{100}\times 600$$
両辺の分母の100をはらい、
両辺を100でわります。
$$\Large 12\times 4=6x$$
両辺を6でわると、
$$\Large 2\times 4=x$$
ゆえに、
$$\Large x=8$$

Lukia
濃度は8%になることがわかりました。
こたえ

Lukia
「水」は、「0%食塩水」という発想があれば、表にも正確に書き込めますね。
また、慣れてくれば、表の一番下の段の「食塩の重さ」のマスに
いきなり「0」を書き込むこともできるようになるでしょう。
現段階では、「食塩水」に「水」を混ぜ合わせる問題は、あと二問用意してありますので、どんどん慣れていってくださいね。
また、慣れてくれば、表の一番下の段の「食塩の重さ」のマスに
いきなり「0」を書き込むこともできるようになるでしょう。
現段階では、「食塩水」に「水」を混ぜ合わせる問題は、あと二問用意してありますので、どんどん慣れていってくださいね。
8%
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません