高校数学の「三角方程式」に関する問題を解いてみる。（Yahoo!知恵袋より）
[mathjax]
\(\frac{1-\sin \theta}{\cos \theta}+\frac{\cos \theta}{1-\sin \theta}\) の値
ハート型の分数にしよう。
れもん
Lukia
分子が二つに書き分けられるようなパターンのことを勝手に「ハート型の分数」と呼ぶことにします。
すると、現在問題の式は、このような形になっていますね。
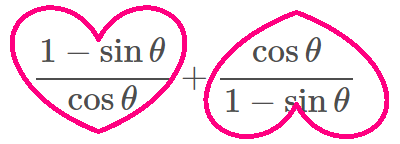
れもん
あ、たしかに、\(\frac{1-\sin \theta}{\cos \theta}=\frac{1}{\cos \theta}-\frac{\sin \theta}{\cos \theta}\) と書き分けられます！
れもん
Lukia
分母を分けることはできませんね。
というわけで、右の「桃型」は、ひと手間かけて「ハート型」に直していきます。
$$\begin{align}\frac{1-\sin \theta}{\cos \theta}&+\frac{\cos \theta}{1-\sin \theta}
\\\\ =&\frac{1}{\cos \theta}-\frac{\sin \theta}{\cos \theta}+\frac{\cos \theta\color{#0004fc}{\left( 1+\sin \theta\right)}}{\left( 1-\sin \theta\right)\color{#0004fc}{\left( 1+\sin \theta\right)}}
\\\\ =&\frac{1}{\cos \theta}-\frac{\sin \theta}{\cos \theta}+\frac{\cos \theta\left( 1+\sin \theta\right)}{\cos^{2} \theta}
\\\\ =&\frac{1}{\cos \theta}-\frac{\sin \theta}{\cos \theta}+\frac{\color{red}{1+\sin \theta}}{\color{red}{\cos \theta}}
\\\\ =&\frac{1}{\cos \theta}-\frac{\sin \theta}{\cos \theta}+\frac{1}{\cos \theta}+\frac{\sin \theta}{\cos \theta}
\\\\ =&\frac{2}{\cos \theta} \end{align}$$
サイン・コサイン・タンジェントは直角三角形を描いて考えろ！
Lukia
式変形をして\(\cos \theta\)の値を求めることは可能ですが、結構時間を喰ってしまうので、
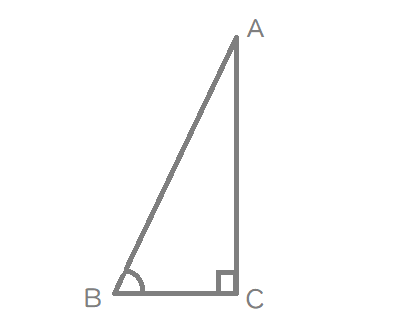
直角三角形を描いて、「三平方の定理」を使って求めてしまいます。
Lukia
\(\tan \theta=\frac{\mathrm{CA}}{\mathrm{BC}}\) より、
辺\(\mathrm{BC}=1\) , 辺\(\mathrm{CA}=5\)と仮定します。
れもん
辺\(\mathrm{AB}=\sqrt{26}\)とわかります。
Lukia
\(\cos \theta=\frac{1}{\sqrt{26}}\) とわかります。
れもん
Lukia
\(1+\tan^{2} \theta=\frac{1}{\cos^{2} \theta}\)を用いるやり方もあります。
しかし、\(\frac{1}{\cos \theta}\)の正負判定をしなければいけないので、結構めんどくさいんですよね。
直角三角形で考えるパターンは、必要があれば辺にマイナスをつければ対応できるので、さっと考えられるという利点があるんです。
これはまた、いい問題があればやってみましょう。
値を求める。
$$\begin{align}与式=&\frac{2}{\cos \theta} \ \\\\ここで、\cos \theta=&\frac{1}{\sqrt{26}} \ より\\\\ =&2\times \left( \frac{1}{\sqrt{26}}\right)^{-1} \\\\ =&2\sqrt{26} \end{align}$$
こたえ
$$2\sqrt{26}$$
共有:
プロフィール
