中学数学の2種類の濃度の食塩水を混ぜる問題（その10）

2018年7月7日2023年1月15日食塩水の濃度実用数学技能検定（数学検定数検),数検3級

読了時間: 約3分44秒

[mathjax]

Lukia

2種類の濃度の食塩水を混ぜ合わせる問題でも、不等式のバージョンを見つけましたので、
載せてみます。
力試しをしてみたい方は、以下に問題を載せていますから、
スクロールの手を止めて、解いてみてください。

問題

濃度13%の食塩水と、濃度5%の食塩水を混ぜ合わせて、
濃度10%以上の食塩水を400g作りたい。
濃度5%の食塩水を何g以下にすればよいか。

表に書き込む。

もも

うわ～、「2種類の濃度の食塩水」の問題、なつかしいわ～。

Lukia

食塩が2回、水が3回でしたから、
5回前ですけど。

もも

いいんですよっ。
さて、さっそく表を描いちゃおう。
まず、横長の線を3本と、それを4等分するように、
縦の線を3本引きます。

Lukia

ももちゃんは、以下のような表を描いています。

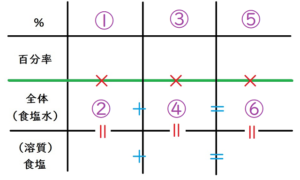
もも

次に、表に文字や数字を書き込んでいきます。
①が13、
③が5、
⑤が10です。

もも

そして、できあがる食塩水の重さが400ｇなので、
⑥が400となります。

もも

問題文を読むと、5%の食塩水の重さを問うようですから、
④に $\Large x$ を入れます。
ということは、全体の重さの段は、「横はたし算」ができるから、
②+④=⑥　が成り立つので、
②は、$\Large \left( 400-x\right)$ とあらわせます。

％を百分率に直しておく。

Lukia

表の①から⑥が書き込めたので、
％を百分率に直していきます。
左から、
$\Large \frac{13}{100}$ ・ $\Large \frac{5}{100}$ ・ $\Large \frac{10}{100}$ となりますね。

もも

あっ、お株を奪われたッ！

縦はかけ算・横はたし算

Lukia

たまにはい～ぢゃないですかぁ。（笑）
では、「縦はかけ算」をお願いします。

もも

（軽く流されたな・・・）
それでは、縦の列ごとに「縦はかけ算」をして、
表の一番下の段のマスをうめていきます。
まず、13%の食塩水の列は、
$\Large \frac{13}{100}\times \left( 400-x\right)$ となります。

Lukia

はいはい♪

もも

むむっ・・・
次に、5%の食塩水の列は、
$\Large \frac{5}{100}\times x$ となります。

Lukia

ヘイヘイ♪

もも

（完全に遊んでるな・・・）
そして、10％の食塩水の列は、
$\Large \frac{10}{100}\times 400$ となります。

Lukia

ホイホイ♪

一番下の段の「たし算」をする。

もも

Lukia先生のことはほっといて、先に進みます。
表の一番下の段は、「横はたし算」をして、式を立てていきます。
ひとまず、
$\Large \frac{13}{100}\times \left( 400-x\right)+\frac{5}{100}\times x=\frac{10}{100}\times 400$ となります。

Lukia

ちなみに、この式は、
「2種類の濃度の食塩水を混ぜ合わせてできる食塩水に含まれる『食塩の重さ』」を表しています。
いま、濃度が10％以上になってほしい。ということは、
左辺と右辺の大小関係はどうなりますか？

もも

いきなりマジメになって復活してこないでくださいッ！

もも

方程式のままだったら、10％きっかりのときの食塩の重さになりますが、
今回はそれよりも多く含まれてほしい。ということなので、
左辺 $\Large \geq $ 右辺が成り立つと思います。

Lukia

そうですね。ですから、不等式の記号を使って、
$\Large \frac{13}{100}\times \left( 400-x\right)+\frac{5}{100}\times x \geq \frac{10}{100}\times 400$ とすることができますね。

もも

じゃ、計算はももがやってみます。
ふきだしははずして書きますね。

$$\Large \frac{13}{100}\times \left( 400-x\right)+\frac{5}{100}\times x \geq \frac{10}{100}\times 400$$
両辺の分母の100をはらって、
$$\Large 13\times \left( 400-x\right)+5x\geq 10\times 400$$
$$\Large \left( 13-10\right)\times 400-13x+5x \geq 0$$

もも

$\Large -8x$ を右辺に移項して

$$\Large 3\times 400 \geq 8x$$
両辺を8でわって、
$$\Large 3\times 50 \geq x$$
$$\Large 150 \geq x 　(または、 x \leq 150 ）$$

もも

つまり、5%の食塩水を150ｇ以下にすればよいことになりますね。

Lukia

よくできました♪