2019年大学入試センター試験数学2B「第2問微分・積分」を解いてみる。

2019年1月25日2023年1月14日大学入試センター試験,微分と積分実用数学技能検定（数学検定数検),数検2級,数検準1級

読了時間: 約7分58秒

問題

$ \ p \ , \ q \ $を実数とし,関数$ \ f\left( x\right)=x^3+px^2+qx \ $は$ \ x=-1 \ $で極値$ \ 2 \ $をとるとする。
また,座標平面上の曲線$ \ y=f\left( x\right) \ $を$ \ \mathrm{C} \ $,放物線$ \ y=-kx^2 \ $を$ \ \mathrm{D} \ $,放物線$ \ \mathrm{D} \ $上の点$ \ \left( a \ , \ -ka^2\right) \ $を$ \ \mathrm{A} \ $とする。
ただし,$ \ k \gt 0 \ , \ a \gt 0 \ $である。
(1)　関数$ \ f\left( x\right) \ $が$ \ x=-1 \ $で極値をとるので,$ \ f’\left( -1\right)=\color{#0004fc}{ア} \ $である。
これと$ \ f\left( -1\right)=2 \ $より,$ \ p=\color{#0004fc}{イ} \ , \ q=\color{#0004fc}{ウエ} \ $である。
よって,$ \ f\left( x\right) \ $は$ \ x=\color{#0004fc}{オ} \ $で極小値$ \ \color{#0004fc}{カキ} \ $をとる。

$$\begin{align}&f’\left( x\right)=0\quad となる \ x \ が極値の \ x \ 座標であるので, \\\\ f’\left( -1\right)=&\color{#0004fc}{0} \\\\ \ ここで,\quad &f’\left( x\right)=3x^2-2px+q\\\\ f’\left( -1\right)=&3+2p+q=0\quad \cdots\cdots \ ⅰ\\\\ f\left( -1\right)=&-1+p-q=2\quad \cdots\cdots \ ⅱ\\\\ &ⅰ, \ ⅱを解いて,\\\\ &p=\color{#0004fc}{0} \ , \ q=\color{#0004fc}{-3}\\\\ 以上より&\mathrm{C}: \ f\left( x\right)=x^3-3x \end{align}$$
$$\begin{align}f’\left( x\right)=&3x^2-3=3\left( x+1\right)\left( x-1\right)\quad より \\\\ f\left( x\right) \ は& \ x=\color{#0004fc}{1} \ で極小値 \ \color{#0004fc}{-2} \ をとる。\end{align}$$

問題

(2)　点$ \ \mathrm{A} \ $における放物線$ \ \mathrm{D} \ $の接線を$ \ l \ $とする。
$ \ \mathrm{D} \ $と$ \ l \ $および$ \ x \ $軸で囲まれた図形の面積$ \ \mathrm{S} \ $を$ \ a \ $と$ \ k \ $を用いて表そう。
$ \ l \ $の方程式は
$ \ y=\color{#0004fc}{クケ}kax+ka^{\color{#0004fc}{コ}}\quad \cdots\cdots \ ① \ $　と表せる。
$ \ l \ $と$ \ x \ $軸の交点の$ \ x \ $座標は$ \ \color{#0004fc}{\frac{サ}{シ}} \ $であり,
$ \ \mathrm{D} \ $と$ \ x \ $軸および直線$ \ x=a \ $で囲まれた図形の面積は$ \ \frac{k}{\color{#0004fc}{ス}}a^{\color{#0004fc}{セ}} \ $である。
よって,　$ \ \mathrm{S}=\frac{k}{\color{#0004fc}{ソタ}}a^{\color{#0004fc}{セ}} \ $　である。

$$\begin{align}l:\quad y=&-2ka\left( x-a\right)-ka^2 \\\\ =&\color{#0004fc}{-2}kax+ka^{\color{#0004fc}{2}}\quad \cdots\cdots \ ① \end{align}$$
$$\begin{align}lと&x軸の交点のx座標を求める。 \\\\ 2kax=&ka^2 \\\\ &k \gt 0 \ , \ a \gt 0 \ より,両辺を \ ka \ で割る。\\\\ x=&\color{#0004fc}{\frac{a}{2}} \end{align}$$
$$\mathrm{D}とx軸および直線 \ x=a \ で囲まれた図形 \ \left( \mathrm{S}’ \ とする\right) \ の面積を求める。$$

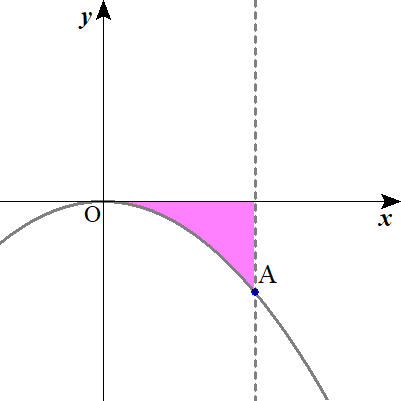
$$\begin{align}\mathrm{S}’=&\int_{0}^{a} kx^2 dx =\left[\frac{k}{3}x^3\right]_{0}^{a}=\frac{k}{\color{#0004fc}{3}}a^{\color{#0004fc}{3}}\end{align}$$

Lukia

問題には、「よって」という言葉で$ \ \mathrm{S} \ $がつながれていますが、
放物線と直線が交点（接点）をひとつもつ場合、3分の1公式が使えますね。
今回はそちらを使います。

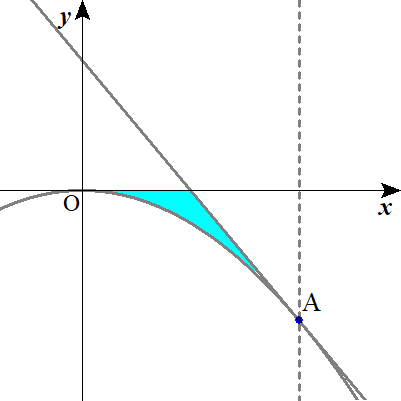
$$\begin{align}\mathrm{S}=&\frac{\vert -k \vert}{3}\left( \frac{a}{2}-0\right)^3=\frac{k}{\color{#0004fc}{24}}a^3 \end{align}$$

問題

(3)　さらに,点$ \ \mathrm{A} \ $が曲線$ \ \mathrm{C} \ $上にあり,かつ(2)の接線$ \ l \ $が$ \ \mathrm{C} \ $にも接するとする。
このときの(2)の$ \ \mathrm{S} \ $の値を求めよう。
$ \ \mathrm{A} \ $が$ \ \mathrm{C} \ $上にあるので,　$ \ k=\color{#0004fc}{\frac{チ}{ツ}}-\color{#0004fc}{テ} \ $　である。

$$\begin{align}-ka^2=&a^3-3a \\\\ ka^2=&-a^3+3a \\\\ k=&\color{#0004fc}{\frac{3}{a}}-\color{#0004fc}{a} \end{align}$$

問題

$ \ l \ $と$ \ \mathrm{C} \ $の接点の$ \ x \ $座標を$ \ b \ $とすると,
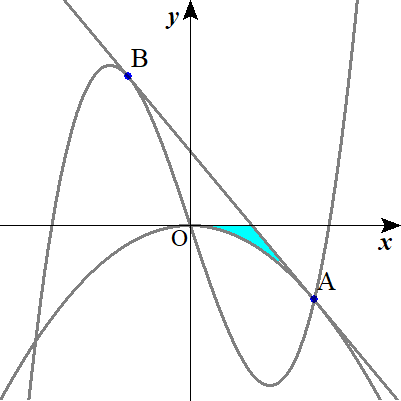
$ \ l \ $の方程式は$ \ b \ $を用いて
$ \ y=\color{#0004fc}{ト}\left( b^2-\color{#0004fc}{ナ}\right)x-\color{#0004fc}{ニ}b^3\quad \cdots\cdots \ ② \ $　と表される。

$$\begin{align}曲線\mathrm{C}と&直線lの接点を \\\\ \mathrm{B}\left( b \ , \ f\left( b\right)\right)\quad とする。 \\\\ l：\quad y=&\left( 3b^2-3\right)\left( x-b\right)+f\left( b\right) \\\\ =&\color{#0004fc}{3}\left( b^2-\color{#0004fc}{1}\right)x-\color{#0004fc}{2}b^3\quad \cdots\cdots \ ② \end{align}$$

問題

②の右辺を$ \ g\left( x\right) \ $とおくと
$ \ f\left( x\right)-g\left( x\right)=\left( x-\color{#0004fc}{ヌ}\right)^2\left( x+\color{#0004fc}{ネ}b\right) \ $
と因数分解されるので、$ \ a=-\color{#0004fc}{ネ}b \ $となる。

$$\begin{align}f\left( x\right)-g\left( x\right)=\left( x-\color{#0004fc}{\alpha}\right)^2\left( x+\color{#0004fc}{\beta}b\right)=&x^3-3b^2x+2b^3 \\\\ x^2の係数より&2\alpha=\beta b \\\\ 定数項より&\alpha^2 \beta b=2b^3\\\\ \alpha^2 \beta b=&\alpha^2\cdot 2\alpha=2b^3\\\\ \alpha=&b\\\\ 2b=&\beta b\quad より\\\\ \beta=&2\\\\ f\left( x\right)-g\left( x\right)&=\left( x-\color{#0004fc}{b}\right)^2\left( x+\color{#0004fc}{2}b\right) \\\\ &a=-\color{#0004fc}{2}b \end{align}$$

問題

①と②の表す直線の傾きを比較することにより,
$ \ a^2=\color{#0004fc}{\frac{ノハ}{ヒ}} \ $　である。

したがって,求める$ \ \mathrm{S} \ $の値は$ \ \color{#0004fc}{\frac{フ}{ヘホ}} \ $　である。

$$\begin{align}-2ka=&3\left( b^2-1\right) \\\\ -2a\left( \frac{3}{a}-a\right)=&3\left( \frac{a^2}{4}-1\right) \\\\ 5a^2=&12\\\\ a^2=&\color{#0004fc}{\frac{12}{5}} \end{align}$$

$$\begin{align}\mathrm{S}=&\frac{k}{24}a^3 \\\\ =&\frac{1}{24}\left( -a^4+3a^2\right) \\\\ =&\frac{1}{24}a^2\left( -a^2+3\right) \\\\ =&\frac{1}{24}\cdot \frac{12}{5}\left( \frac{-12+15}{5}\right)\\\\ =&\color{#0004fc}{\frac{3}{50}} \end{align}$$

Lukia

オーソドックスな問題だったと思います。
ただ、計算がめんどくさいですね。
ちなみに、正確なグラフを描画ソフト「GRAPES」で描くため、曲線や直線、点A,Bなどを算出してみました。
どえらい数字でしたよ。（笑）
$ \ \mathrm{C}: \ f\left( x\right)=x^3-3x $
$ \ \mathrm{D}: \ y=-\frac{3}{2\sqrt{15}}x^2 \ $
$ \ l: \ y=-\frac{6}{5}x+\frac{6\sqrt{15}}{25} \ $
$ \ \mathrm{A}: \ \left( \frac{2\sqrt{15}}{5} \ , \ -\frac{6\sqrt{15}}{25}\right) \ $
$ \ \mathrm{B}: \ \left( -\frac{\sqrt{15}}{5} \ , \ \frac{12\sqrt{15}}{25}\right) \ $

2019年大学入試センター試験の数学の問題の一覧です。