2019年大学入試センター試験数学1A「第1問数と式」を解いてみる。

2019年1月25日2023年1月14日大学入試センター試験,数と式実用数学技能検定（数学検定数検),数検準2級

読了時間: 約4分45秒

[mathjax]

問題

$ \ a \ $を実数とする。
$ \ 9a^2-6a+1=\left( \color{#0004fc}{ア}a-\color{#0004fc}{イ}\right)^2 \ $　である。
次に　$ \ \mathrm{A}=\sqrt{9a^2-6a+1}+\vert a+2 \vert \ $　とおくと
$ \ \mathrm{A}=\sqrt{\left( \color{#0004fc}{ア}a-\color{#0004fc}{イ}\right)^2}+\vert a+2 \vert \ $　である。

$$\begin{align}9a^2-6a+1=&\left( \color{#0004fc}{3}a-\color{#0004fc}{1}\right)^2 \end{align}$$
ここで,
$$\begin{align}\left( 3a-1\right)^2=&k^2\quad \left( k \geq 0\right) \quad とすると,\\\\ k=& \pm \left( 3a-1\right)=\vert 3a-1 \vert \ \\\\ ゆえに,\quad \mathrm{A}=&\sqrt{\left( 3a-1\right)^2}+\vert a+2 \vert\\\\ =&\vert 3a-1 \vert +\vert a+2 \vert \end{align}$$

ディノ

うおぉ～～～！絶対値だ～～～！

Lukia

でぃ、ディノさん・・・。
突然出てきたら、当ブログ初めての方は、驚いちゃいますよ？

Lukia

当記事をお読みの皆様、彼は、恐竜高校生のディノさんです。
私が異世界に紛れ込んでしまい、その時に出会ったという設定になっています。
彼は、絶対値の問題を解くとき、よく現れます。
ちなみに、ディノさんは、スイーツ好きです。（笑）

問題

次の三つの場合に分けて考える。
・$ \ a \gt \frac{1}{3} \ $のとき,$ \ \mathrm{A}=\color{#0004fc}{ウ}a+\color{#0004fc}{エ} \ $　である。
・$ \ -2 \leq a \leq \frac{1}{3} \ $のとき,$ \ \mathrm{A}=\color{#0004fc}{オカ}a+\color{#0004fc}{キ} \ $　である。
・$ \ a \lt -2 \ $のとき,$ \ \mathrm{A}=-ウa-エ \ $　である。

ディノ

センター試験にも出るんだな！絶対値！

Lukia

そうですねぇ。平方根をはずしたら、絶対値が表れる。というところは、
ちょっとめんくらった人がいるんじゃないかなと思いますね。

ディノ

ま、でも、この記事で、グラフの描き方を覚えてしまえば、次からは楽になるかもな。

ディノ

まずは、絶対値のだいたいのグラフを描くんだ。
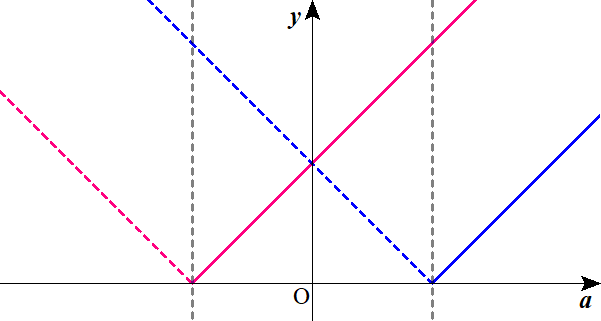
ピンクの実線・点線が$ \ y=\vert a+2 \vert \ $　だ。
絶対値は、$ \ 0 \ $すなわち,$ \ a \ $軸までの距離（大きさ）だから,マイナスになることはありえねぇよな。
そんなわけで,マイナスの値を取っていた実線のグラフは、$ \ a \ $軸でパタンと折れ曲がって、点線の方向で伸びていくわけだ。
同様に青の実線・点線が$ \ y=\vert 3a-1 \vert \ $　だ。
実際のグラフは、ピンクのグラフよりも鋭角なんだけど、この際気にするな。

Lukia

ほぉほぉ。
ちなみに、$ \ a \ $軸と交わっているところの$ \ a \ $座標は？

ディノ

それは、$ \ 3a-1=0 \ $と$ \ a+2=0 \ $を解いて、
$ \ a=\color{#0004fc}{\frac{1}{3}} \ $と$ \ a=\color{#f700ca}{-2} \ $を出せばいい。

Lukia

ディノさん、たのもしぃ～～～！
次は？

ディノ

オマエ、オレに全部やらせて楽しようとしてるな。
ま、いいか。
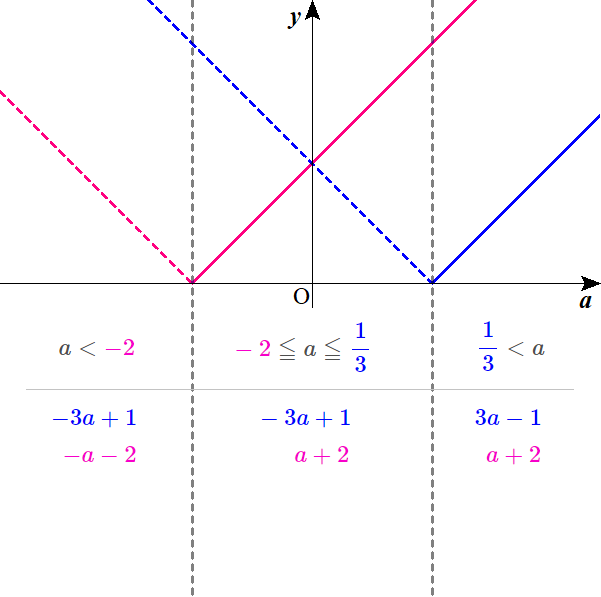
次は、グラフのように、$ \ a=\color{#0004fc}{\frac{1}{3}} \ $と$ \ a=\color{#f700ca}{-2} \ $のところで、線をひっぱっておくんだ。
図だと灰色の点線な。
これによって、$ \ ay \ $平面が3つの範囲にわけられたことになる。
$ \ a \ $軸の下の部分に、具体的な式を書きこむから、余裕をもたせておいてくれよな。

ディノ

そして,グラフに合うように式を書き込んでいくんだ。
点線はそれぞれ、$ \ y=\color{#f700ca}{-a-2} \ $と$ \ y=\color{#0004fc}{-3a+1} \ $になるよな。

Lukia

ほぉほぉ。そして？

ディノ

$ \ \mathrm{A} \ $は二つの絶対値の和だったんだから、青の式とピンクの式を筆算するだけだ。

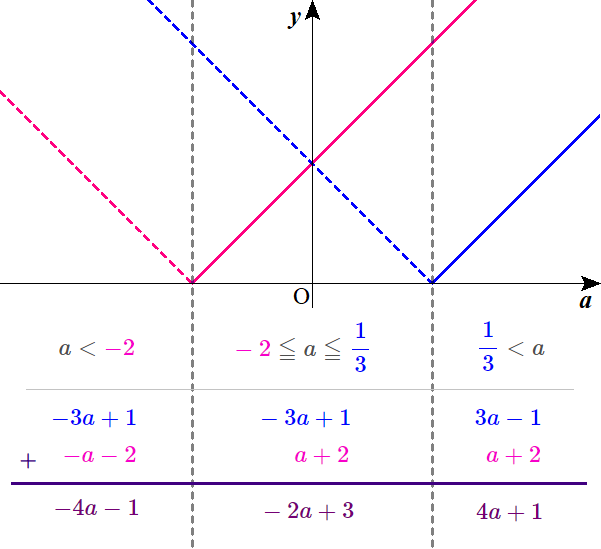
$$\begin{align}a \gt \frac{1}{3} \ のとき,& \ \mathrm{A}=\color{#0004fc}{4}a+\color{#0004fc}{1} \\\\ -2 \leq a \leq \frac{1}{3} \ のとき,& \ \mathrm{A}=\color{#0004fc}{-2}a+\color{#0004fc}{3} \\\\ a \lt -2 \ のとき,& \ \mathrm{A}=-4a-1 \end{align}$$

問題

$ \ \mathrm{A}=2a+13 \ $となる$ \ a \ $の値は　$ \ \color{#0004fc}{ク} \ , \ \color{#0004fc}{\frac{ケコ}{サ}} \ $　である。

Lukia

本当は、下のようなグラフが描けたらいいのですが、
時間的にも、紙面的な余裕もないので、
この場合は、それぞれ$ \ a \ $に関する方程式を解いて、それらが範囲と合致しているかを確かめたほうが速いし、確実だろうと思います。

$$\begin{align}-2 \lt a\quad のとき \ &\quad 2a+13=-4a-1 \\\\ &a=-\frac{7}{3} \\\\ \ -2 \leq a \leq \frac{1}{3}\quad のとき \ & \ 2a+13=-2a+3\\\\ &a=-\frac{5}{2}\quad 範囲に合致しないので不適.\\\\ \ \frac{1}{3} \lt a\quad のとき \ & \ 2a+13=4a+1\\\\ &a=6 \end{align}$$
$$以上より,\quad a=\color{#0004fc}{6} \ , \ \color{#0004fc}{\frac{-7}{3}}$$