2019年大学入試センター試験 数学1A「第2問 データの分析(箱ひげ図と散布図)」を解いてみる。

読了時間: 約2分44秒
[mathjax]
問題
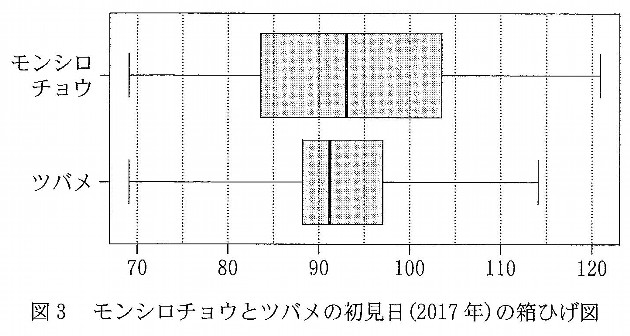
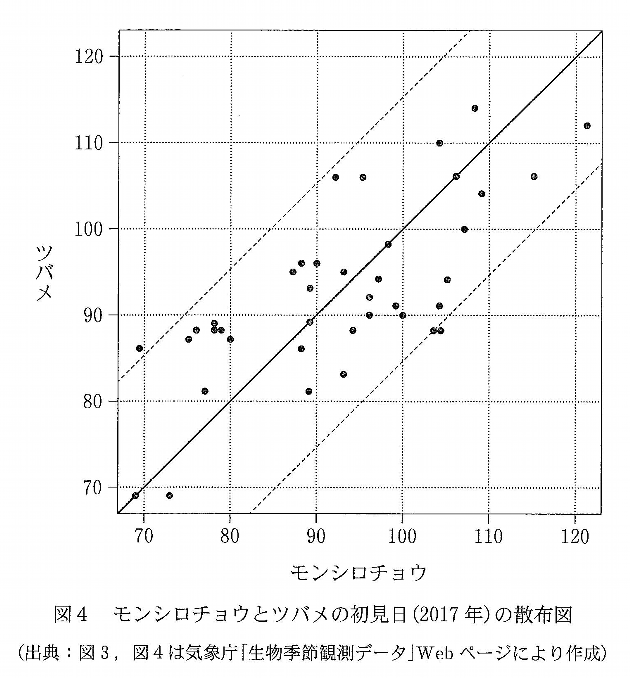
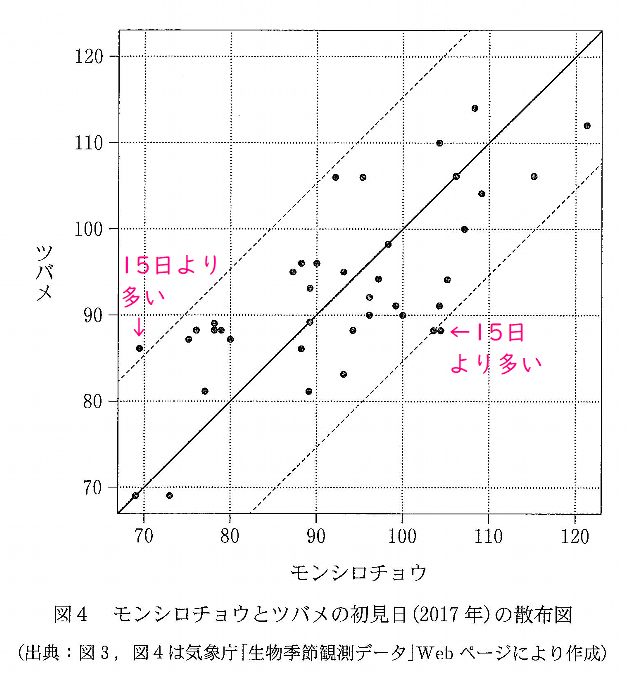
(2) 図3と図4は,モンシロチョウとツバメの両方を観測している41地点における,2017年の初見日の箱ひげ図と散布図である。散布図の点には重なった点が2点ある.なお,散布図には原点を通り傾き\( \ 1 \ \)の直線(実線),切片が\( \ -15 \ \)および\( \ 15 \ \)で傾きが\( \ 1 \ \)の2本の直線(破線)を付加している。
問題
以下の8つの選択肢のうち、図3と図4から読み取れることとして正しくないものは,\( \ \color{#0004fc}{チ} \ \)と\( \ \color{#0004fc}{ツ} \ \)である。
⓪ モンシロチョウの初見日の最小値はツバメの初見日の最小値と同じである。
① モンシロチョウの初見日の最大値はツバメの初見日の最大値より大きい。
② モンシロチョウの初見日の中央値はツバメの初見日の中央値より大きい。
③ モンシロチョウの初見日の四分位範囲はツバメの初見日の四分位範囲の3倍より小さい。
④ モンシロチョウの初見日の四分位範囲は15日以下である。
⑤ ツバメの初見日の四分位範囲は15日以下である。
⑥ モンシロチョウとツバメの初見日が同じ所が少なくとも4地点ある。
⑦ 同一地点でのモンシロチョウの初見日とツバメの初見日の差は15日以下である。

Lukia
選択肢の⓪から⑤までは図3を読み解くことで正誤判定ができそうですね。

⓪と①は正しい.
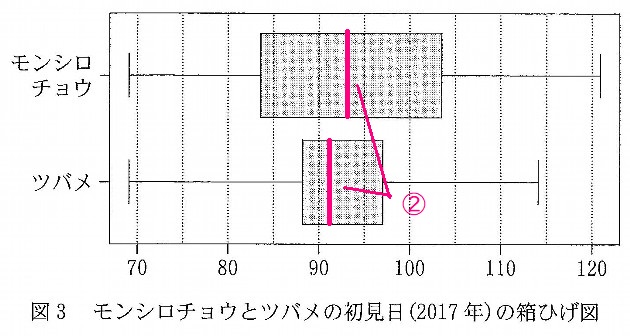
②は正しい。

Lukia
四分位範囲とは、箱ひげ図で黒っぽく塗りつぶされた箱の部分の両端の値の差を指します。
モンシロチョウの四分位範囲は、\( \ 103-83=20 \ \)で(数値は目測によるもので正確ではありません)\( \ 20 \ \)
ツバメの四分位範囲は、\( \ 97-87=10 \ \)で\( \ 10 \ \)となります。
モンシロチョウの四分位範囲は、\( \ 103-83=20 \ \)で(数値は目測によるもので正確ではありません)\( \ 20 \ \)
ツバメの四分位範囲は、\( \ 97-87=10 \ \)で\( \ 10 \ \)となります。

Lukia
ツバメの四分位範囲の3倍は\( \ 10\times 3=30 \ \)となり,
モンシロチョウの四分位範囲\( \ 20 \ \)は明らかに小さいですね。
モンシロチョウの四分位範囲\( \ 20 \ \)は明らかに小さいですね。
③は正しい。
モンシロチョウの初見日の四分位範囲は,
$$103-83=20\quad より,$$
④は誤りである。
ツバメの初見日の四分位範囲は,
$$97-87=10\quad より,$$
⑤は正しい。

Lukia
⑥以降は、図4をもとに考えていきます。
モンシロチョウとツバメの初見日が同じということは、原点を通り、傾き\( \ 1 \ \)の直線上に、点があるということです。
実際、数えてみると4点ありますね。
ちなみに、「少なくとも4点」と書いてあるのは、観測した41地点のうち、重なったところが2点ある。とことわってあるからなんですね。
もしかしたら、この4点のうちにも、重なった地点が表現されているかもしれないので、わざわざ「少なくとも」と書いてあるわけです。
モンシロチョウとツバメの初見日が同じということは、原点を通り、傾き\( \ 1 \ \)の直線上に、点があるということです。
実際、数えてみると4点ありますね。
ちなみに、「少なくとも4点」と書いてあるのは、観測した41地点のうち、重なったところが2点ある。とことわってあるからなんですね。
もしかしたら、この4点のうちにも、重なった地点が表現されているかもしれないので、わざわざ「少なくとも」と書いてあるわけです。
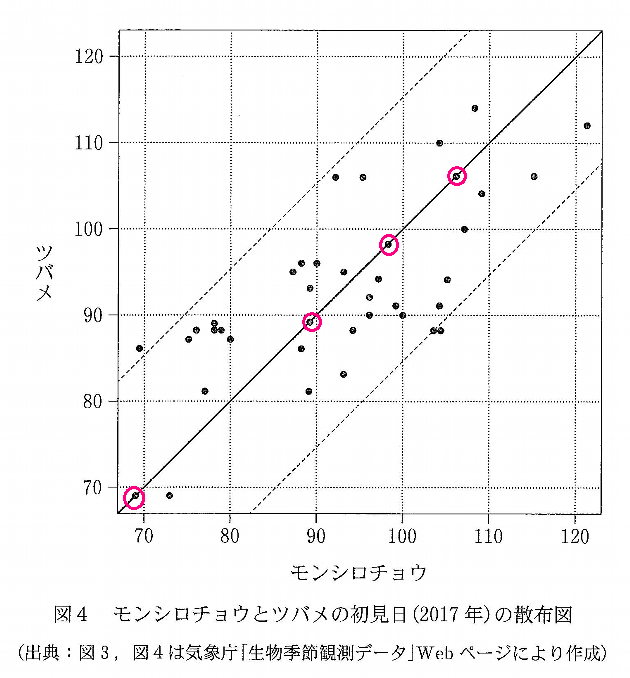
⑥は正しい。

Lukia
「⑥が正しいとわかったんだから、⑦が間違いでいいじゃ~ん。」
本番ではそれでいいと思います。
しかし、まだ試験まで余裕のある方は、どうして⑦が間違いなのか、見てみましょう。
本番ではそれでいいと思います。
しかし、まだ試験まで余裕のある方は、どうして⑦が間違いなのか、見てみましょう。

Lukia
問題のはじめの方に書いてあった、傾き\( \ 1 \ \)で切片が\( \ \pm 15 \ \)の破線が、ここで活きてきます。
傾き\( \ 1 \ \)の実線と、2本の破線は幅15を保って平行に走っています。
つまり、実線から始まり、破線を通り越すと、初見日の差は15日よりも多いことになります。
傾き\( \ 1 \ \)の実線と、2本の破線は幅15を保って平行に走っています。
つまり、実線から始まり、破線を通り越すと、初見日の差は15日よりも多いことになります。

Lukia
図4を見てみると、初見日の差が15日よりも多いところが、「少なくとも」2地点あるとわかりますね。
⑦は誤りである。
以上より,図4から読み取れることとして正しくないものは,
$$\color{#0004fc}{④}\quad と\quad \color{#0004fc}{⑦}\quad である。$$
2019年大学入試センター試験の数学の問題の一覧です。
2019年1月20日に実施された大学入試センター試験の数学1Aのデータの分析の問題を解いてみました。











ディスカッション
コメント一覧
まだ、コメントがありません