高校数学の「平面ベクトルにおける点の存在範囲」に関する問題を解いてみる。（Yahoo!知恵袋より）

2019年1月11日2023年1月14日ベクトル実用数学技能検定（数学検定数検),数検2級,数検準1級

読了時間: 約2分19秒

[mathjax]

問題

O

を原点とする座標平面上に点

A (1, 1)

B (- 2, 4)

がある.
また,点

P

を

\vec{OP} = s \vec{OA} + t \vec{OB}

(

s, t

は実数）で定める.
(1)　

s = 1, t = \frac{1}{2}

のとき,点

P

の座標を求めよ.
(2)　

s, t

が,

0 \leq s \leq 2, 0 \leq t \leq 1

を満たして変化するとき,点

P

が存在する範囲を求めてそれを図示せよ.
(3)　

s, t

が,

s + t = 1, s \geq 0, t \geq 0

を満たして変化するとき,点

P

が存在する範囲を求めてそれを図示せよ.
(4)　

s, t

が,

s + t = \frac{1}{2}, s \geq 0, t \geq 0

を満たして変化するとき,点

P

が存在する範囲を求めてそれを図示せよ.

(1)を解く。

$\begin{aligned} \vec{OP} = & \vec{OA} + \frac{1}{2} \vec{OB} \\ = & (1 - 1, 1 + 2) \\ = & (0, 3) \end{aligned}$

(2)を解く。

$\begin{aligned} \vec{OP} = & s \vec{OA} + t \vec{OB} \\ (0 \leq s \leq 2, 0 \leq t \leq 1) \end{aligned}$
点Pは平行四辺形BOCDの周上とその内部

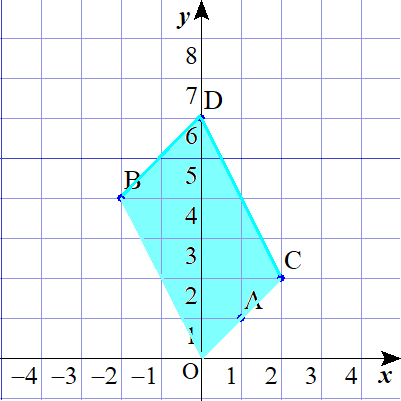
(3)を解く。

点Pは線分AB上（端点A, Bを含む）

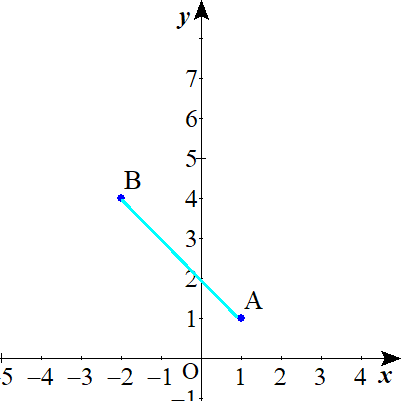
(4)を解く。

$\begin{aligned} s + t = & \frac{1}{2} \\ 2 s + 2 t = & 1 \\ \vec{OP} = & 2 s \cdot \frac{1}{2} \vec{OA} + 2 t \cdot \frac{1}{2} \vec{OB} \\ ここで, & 2 s = k とする . \\ \vec{OP} = & k \cdot \frac{1}{2} \vec{OA} + (1 - k) \cdot \frac{1}{2} \vec{OB} \end{aligned}$
点Pは線分CD上。（端点C, Dを含む）

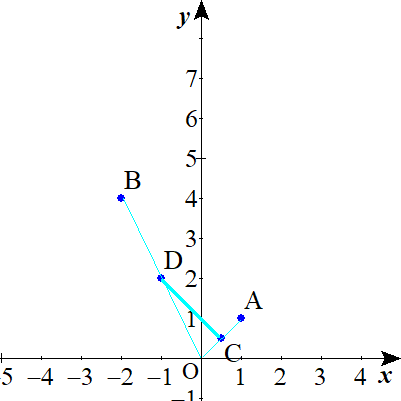
こたえ

今回は省略します。
上記を参考にしてください。

関連

プロフィール

Author Profile

Lukia_74

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。

カテゴリー