Yahoo!知恵袋の高校数学カテゴリにあった「指数・対数」に関する問題を解いてみる。

2018年10月3日2023年1月15日指数と対数実用数学技能検定（数学検定 数検),数検2級

[mathjax]

解法

Lukia

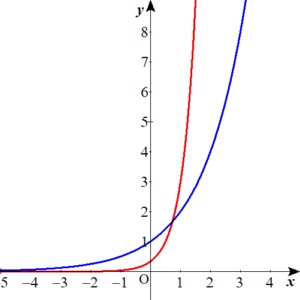
ちなみに、両辺それぞれのグラフは上の図のとおり。
青が左辺の\(y=2^x\) , 赤が右辺の\(y=3^{2x-1}\)　です。
青の曲線と赤の曲線が交わるところを求めます。

Lukia

いろんなやり方があると思いますが、私は、両辺に\(x\)がちらばっているのがいやだったので、なんとか一つにまとめられないか。それぞれ似たような形にならないかを考えることにしました。

$$\begin{align}両辺に3をかける。　& \\\\ 3\cdot 2^x=&3^{2x-1\color{red}{+1}} \\\\ 3\cdot 2^x=&3^{2x} \end{align}$$
ここで、右辺は
$$3^{2x}=\left( 3^2\right)^{x}$$
であるから、
$$3\cdot 2^x=9^x$$

Lukia

両辺とも\(〇^x\)　という形になりました。
いよいよ一つにまとめたいのですが、
ここで問題となるのは、\(\color{red}{はたして「両辺を2^xで割っていいのか。」}\)ということです。
というのも、もし\(2^x\)が\(0\)になることもあったら、割れませんからね。

Lukia

ここで、ちょっとグラフの助けを借りてみます。
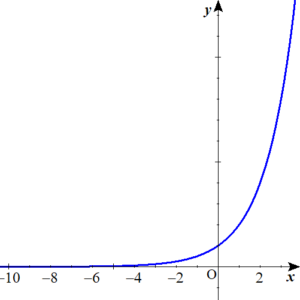
以下の図は、\(y=2^x\)のグラフです。

Lukia

\(x\)の値が、\(0\)を超え、マイナスになっても、
\(y\)の値は、ギリッギリ\(0\)よりも少し上をたどっています。
限りなく\(0\)には近づくのですが、\(\color{red}{完全に0になることはありません。}\)

Lukia

すなわち、
\(\Large 2^x \gt 0\)
がいえます。

$$\begin{align}3\cdot 2^x=&9^x \\\\ ここで、2^x \gt 0&より、両辺を2^x で割って、 \\\\ \left( \frac{9}{2}\right)^x=&3 \end{align}$$
ここで、両辺の常用対数を取ると、
$$\begin{align}\log_{10}\left( \frac{9}{2}\right)^x=&\log_{10}3 \\\\ x=&\frac{\log_{10}3}{\log_{10}\frac{9}{2}} \end{align}$$

こたえ

$$x=\frac{\log_{10}3}{\log_{10}\frac{9}{2}} $$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。