高校数学の「メネラウスの定理」に関する問題を解いてみる。（Yahoo!知恵袋より）

2018年12月24日2023年1月14日図形と計量実用数学技能検定（数学検定 数検),数検準2級

[mathjax]

問題

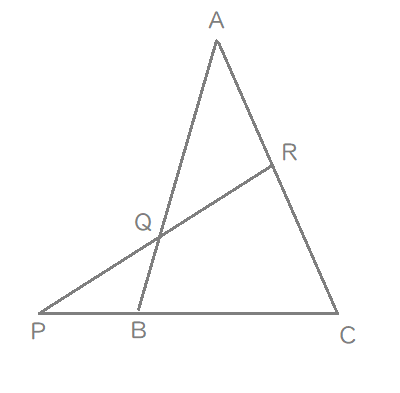
下の図の\(\triangle \mathrm{ABC}\)において、
\(\mathrm{PB}:\mathrm{BC}=1:2\) , \(\mathrm{CR}:\mathrm{RA}=4:3\)である。
\(\mathrm{PQ}:\mathrm{QR}\)を求めよ。

唱えよ！そしてなぞれ！

Lukia

「メネラウスの定理」ということを覚えても、
使えなければ意味がありません。
私は、「子し・母ぼ・子し・母ぼ・子し・母ぼ！」と呪文のように唱えながら、図の上をなぞって覚えました。

「メネラウスの定理」

$$\frac{\mathrm{AR}}{\mathrm{RC}}\times \frac{\mathrm{CP}}{\mathrm{PB}}\times \frac{\mathrm{BQ}}{\mathrm{QC}}=1$$

あれ？そのままじゃ解けない？

Lukia

図形を見れば、「メネラウスの定理」を使うことを思いつきます。
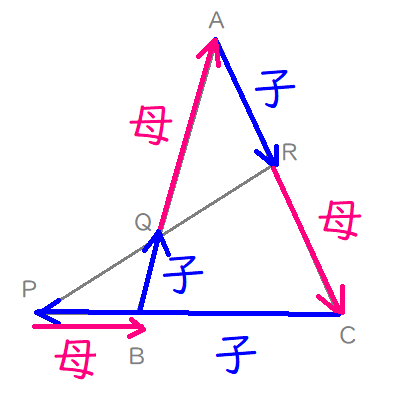
上の図で、頂点\(\mathrm{A}\)から始まり、再び頂点\(\mathrm{A}\)に戻ってくるように「メネラウスの定理」をあてはめ、
「子・母・子・母・・・」と唱えながら、図形をなぞってみました。
しかし、頂点\(\mathrm{A}\)から始めると、比を求める2つの線分を通らず、灰色のまま残ってしまいました。

Lukia

通常、「メネラウスの定理」を練習させる問題は、図の上方にある頂点からくるっと一周するように作られているのですが、
この問題は、ちょっとあまのじゃくですね。
今回は、頂点\(\mathrm{P}\)から始めて、再び頂点\(\mathrm{P}\)に戻ってくるように「メネラウスの定理」をあてはめなければなりませんでした。
図の上方から一周するのに慣れている人、また、「メネラウスの定理」そのものが習いたてで余裕のない人は、時計回りに\(90^{\circ}\)回転させてみましょう。
首を横に曲げるより、解きやすくなりますよ。

ではあらためて「メネラウスの定理」にあてはめていく。

Lukia

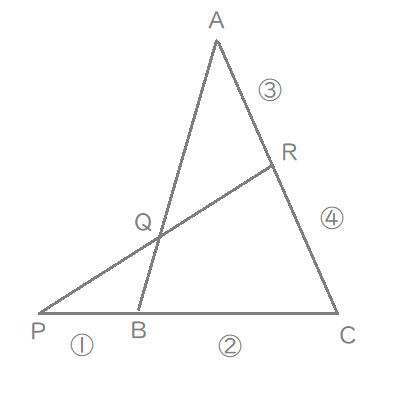
まずは、わかっている線分比を書き込んでみます。

Lukia

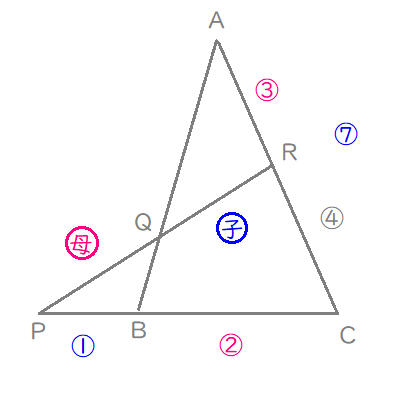
呪文を唱えながら、線分の一部を書き換えます。(笑)

Lukia

あとは、「呪文」を数学語に変えましょう。

「メネラウスの定理」より
$$\begin{align}\frac{\mathrm{PB}}{\mathrm{BC}}\times \frac{\mathrm{CA}}{\mathrm{AR}}\times \frac{\mathrm{RQ}}{\mathrm{QP}}=&1 \\\\ \frac{1}{2}\times \frac{7}{3}\times \frac{\mathrm{RQ}}{\mathrm{QP}}=&1 \\\\ \mathrm{PQ}:\mathrm{QR}=&7:6 \end{align}$$

こたえ

$$\mathrm{PQ}:\mathrm{QR}=7:6$$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。