Yahoo!知恵袋の高校数学カテゴリにあった「三角比と図形」に関する問題を解いてみる。

2018年9月29日2023年1月15日図形と計量実用数学技能検定（数学検定 数検),数検準2級

[mathjax]

問題

次の図形において、\(\mathrm{AD}\)の長さを求めよ。

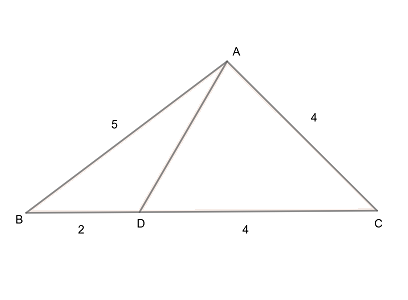
解法

$$\begin{align}\angle\mathrm{ADC}=&\theta　とすると、\\\\ \angle\mathrm{ADB}=&\pi-\angle\mathrm{ADC} \\\\ =&\pi-\theta　が成り立つ。\\\\  \ ゆえに、\\\\ \cos \angle\mathrm{ADB}=&\cos \left( \pi-\theta\right)\\\\ =&-\cos \theta \end{align}$$

$$\begin{align}ここで、\mathrm{AD}=&x \left( x \gt 0\right) とする。\\\\ 余弦定理より&\\\\ \cos \theta=&\frac{4^2+x^2-4^2}{2\cdot 4\cdot x} \cdots①\\\\ \cos \left( \pi-\theta\right)=&\frac{2^2+x^2-5^2}{2\cdot 2\cdot x} \cdots②\\\\ ②\times \left( -1\right)=&①　より\\\\ -\left( \frac{2^2+x^2-5^2}{2\cdot 2\cdot x}\right)=&\frac{4^2+x^2-4^2}{2\cdot 4\cdot x} \end{align}$$
$$\begin{align}-\color{red}{2}\left( x^2-21\right)=&x^2 \\\\ -3x^2=&-42\\\\ x^2=&14\\\\ x=& \pm \sqrt{14} \\\\ ただし、x \gt &0 より\\\\ x=&\sqrt{14} \end{align}$$
$$\Large ゆえに、\mathrm{AD}=\sqrt{14}$$

こたえ

$$\Large \mathrm{AD}=\sqrt{14}$$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。