高校数学の「平面ベクトル（書き換え練習）」に関する問題を解いてみる。（Yahoo!知恵袋より）

2018年12月17日2023年1月14日ベクトル実用数学技能検定（数学検定 数検),数検2級,数検準1級

[mathjax]

(1)を解く。

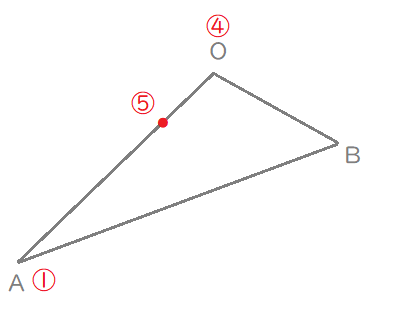
$$\overrightarrow{\mathrm{OC}}=\frac{1}{5}\overrightarrow{\mathrm{OA}}$$

$$\begin{align}\\\\ 2\overrightarrow{\mathrm{AP}}+3\overrightarrow{\mathrm{BP}}=&\overrightarrow{\mathrm{0}} \\\\ 2\overrightarrow{\mathrm{OP}}-2\overrightarrow{\mathrm{OA}}+3\overrightarrow{\mathrm{OP}}-3\overrightarrow{\mathrm{OB}}=&\overrightarrow{\mathrm{0}} \\\\ 5\overrightarrow{\mathrm{OP}}=&2\overrightarrow{\mathrm{OA}}+3\overrightarrow{\mathrm{OB}}\\\\ \overrightarrow{\mathrm{OP}}=&\frac{1}{5}\left( 2\overrightarrow{\mathrm{OA}}+3\overrightarrow{\mathrm{OB}}\right) \end{align}$$

Lukia

全体としてベクトルを別のベクトルを使って表現しなおすだけなので、
平面ベクトルの中でも、かなり基礎的な問題であるといえます。

(2)を解く。

$$\begin{align}\overrightarrow{\mathrm{QC}}=&\overrightarrow{\mathrm{OC}}-\overrightarrow{\mathrm{OQ}} \\\\ =&\frac{1}{5}\overrightarrow{\mathrm{OA}}-3\overrightarrow{\mathrm{OP}} \\\\ =&\frac{1}{5}\left( \overrightarrow{\mathrm{OA}}-6\overrightarrow{\mathrm{OA}}-9\overrightarrow{\mathrm{OB}}\right)\\\\ =&-\frac{1}{5}\left( 5\overrightarrow{\mathrm{OA}}+9\overrightarrow{\mathrm{OB}}\right) \end{align}$$
$$\begin{align}\vert \overrightarrow{\mathrm{OP}} \vert^2=&\frac{4}{25}\vert\overrightarrow{\mathrm{OA}} \vert^2+2\cdot \frac{3}{25}\overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}}+\frac{9}{25}\vert\overrightarrow{\mathrm{OB}} \vert^2 \\\\ \frac{13}{25}=&\frac{1}{25}\left( 16+12\overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}}+9\right) \\\\ 12\overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}}=&-25+13=-12\\\\ \overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}}=&-1 \end{align}$$

Lukia

\(\frac{\overrightarrow{\mathrm{OA}}\cdot \overrightarrow{\mathrm{OB}}}{\vert \overrightarrow{\mathrm{OA}} \vert\vert \overrightarrow{\mathrm{OB}} \vert}=-\frac{1}{2}\)より、
辺\(\mathrm{OA}\)と辺\(\mathrm{OB}\)のなす角は\(120^{\circ}\)とわかります。

(3)を解く。

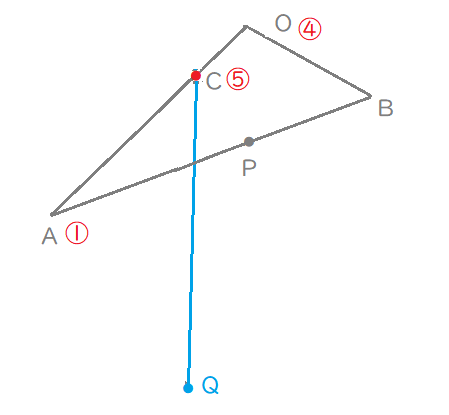
Lukia

図によると、辺\(\mathrm{OA}\)と直線\(\mathrm{CQ}\)が交わるのは、
点\(\mathrm{C}\)のみなので・・・

$$\overrightarrow{\mathrm{OR}}=\overrightarrow{\mathrm{OC}}=\frac{1}{5}\overrightarrow{\mathrm{OA}}$$

$$\begin{align}\overrightarrow{\mathrm{OQ}}\cdot \overrightarrow{\mathrm{OR}}=&3\overrightarrow{\mathrm{OP}}\cdot \frac{1}{5}\overrightarrow{\mathrm{OA}} \\\\ =&\frac{1}{5}\left( 6\overrightarrow{\mathrm{OA}}+9\overrightarrow{\mathrm{OB}}\right)\cdot \frac{1}{5}\overrightarrow{\mathrm{OA}} \\\\ =&\frac{1}{25}\left( 6\cdot 4+9\cdot \left( -1\right)\right)\\\\ =&\frac{15}{25} \\\\ =&\frac{3}{5} \end{align}$$

こたえ

(1)
$$\overrightarrow{\mathrm{OC}}=\frac{1}{5}\overrightarrow{\mathrm{OA}}$$
$$\overrightarrow{\mathrm{OP}}=\frac{1}{5}\left( 2\overrightarrow{\mathrm{OA}}+3\overrightarrow{\mathrm{OB}}\right)$$
(2)
$$\overrightarrow{\mathrm{QC}}=-\frac{1}{5}\left( 5\overrightarrow{\mathrm{OA}}+9\overrightarrow{\mathrm{OB}}\right)$$
(3)
$$\overrightarrow{\mathrm{OR}}=\frac{1}{5}\overrightarrow{\mathrm{OA}}$$
$$\overrightarrow{\mathrm{OQ}}\cdot \overrightarrow{\mathrm{OR}}=\frac{3}{5} $$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。