高校数学の「絶対値がらみの積分」に関する問題を解いてみる。（Yahoo!知恵袋より）
\(\int_0^a \vert x-2 \vert dx=\int_0^2 \vert x-a \vert dx\)を満たす\(a\)の値を求めよ。
まずは左辺から整理してみる。
Lukia
おおまかなグラフで考えてみましょう。
なお、グラフ中の\(x\)軸に打ってある目盛りは正確ではないことをご了承くださいね。
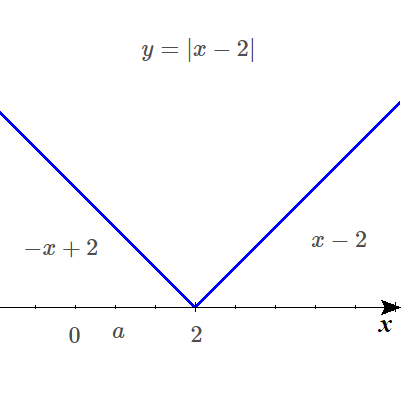
$$\begin{align}\int_0^a \vert x-2 \vert dx=&\int_0^a\left( -x+2\right) dx\\\\ =&\left[-\frac{1}{2}x^2+2x\right]_0^a \\\\ =&-\frac{1}{2}a^2+2a\end{align}$$
右辺の整理をする。
$$y=\vert x-a \vert\quad のグラフは以下の通り.$$
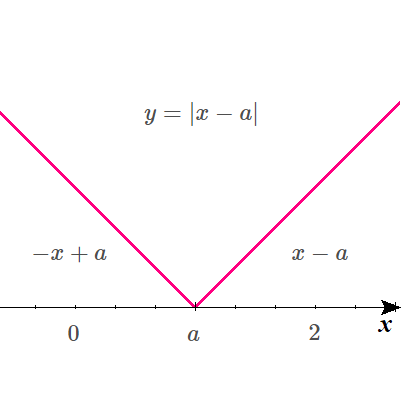
$$\begin{align}ここで, \ g\left( x\right)=&x-a \ とし, \\\\ g\left( x\right) \ の原関数を&G\left( x\right) \ とおく. \\\\ \int_0^2 \vert x-a \vert dx=&-\int_0^a g\left( x\right) dx+\int_a^2 g\left( x\right) dx\\\\ =&-G\left( a\right)+G\left( 0\right)+G\left( 2\right)-G\left( a\right)\\\\ =&-2G\left( a\right)+G\left( 0\right)+G\left( 2\right)\\\\ ここで,G\left( x\right)=&\frac{1}{2}x^2-ax\quad であるから,\\\\ 与式=&a^2-2a+2\end{align}$$
aに関する二次方程式を解く。
$$\begin{align}-\frac{1}{2}a^2+2a=&a^2+2-2a\ 3a^2-8a+4=&0 \\\\ \left( 3a-2\right)\left( a-2\right)=&0\ \\\\ &a=\frac{2}{3}, \ a=2\\\\ ただし,&0 \lt a \lt 2 \ より\\\\ a=&\frac{2}{3} \end{align}$$
Lukia
絶対値を単なる数式で解こうとすると、イメージが湧かないため、大変苦労すると思います。
当ブログにも、絶対値に関する問題を解いた記事がいろいろありますから、いくつかお読みになり、絶対値に対する苦手意識を低減させてください。
ディノ
Lukia
なぜここに・・・
ディノ
なんで一人で解いてんだよ。
しかもこれ、見たことある記号がついてるヤツじゃんよ。
Lukia
ディノ
あ、そういえば、オレのなじみのワッフル屋が、いちごフェアやってんだよ。
行くぞ！
Lukia
こたえ
$$a=\frac{2}{3}$$
共有:
プロフィール
