高校数学の「放物線と直線のなす領域」に関する問題を解いてみる。（Yahoo!知恵袋より）
[mathjax]
(1) 点\(\mathrm{P} \ \left( x \ , \ y\right)\)が領域\(\mathrm{D}\)を動くとき、\(\mathrm{P}\)の\(x\)座標の最小値、最大値を求めよ。
(2) 点\(\mathrm{P} \ \left( x \ , \ y\right)\)が領域\(\mathrm{D}\)を動くとき、\(x-\frac{1}{18}y\)の最小値、最大値を求めよ。
まずは領域を描いてみよう。
連立不等式のそれぞれを書き直してみます。
$$\begin{align}18x^2-y-1 \leq 0\quad \quad →\quad &18x^2-1 \leq y \\\\ 6x-y+3 \geq 0\quad \quad →\quad &6x+3 \geq y\end{align}$$
Lukia
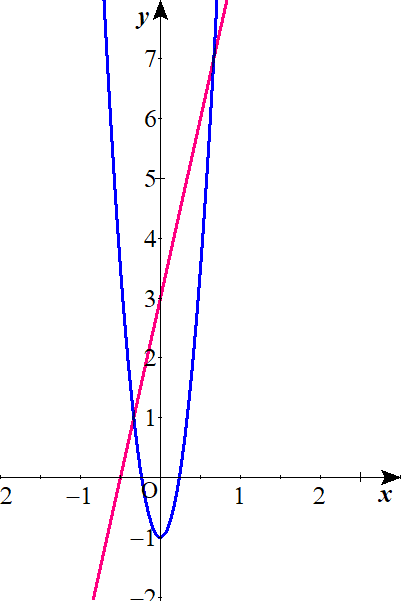
Lukia
青い放物線の内側とピンクの直線の下側の重なった部分であるとわかります。
$$求める領域\mathrm{D}は \ 以下の図の紫色で塗りつぶされた部分である.\left( 境界を含む.\right)$$
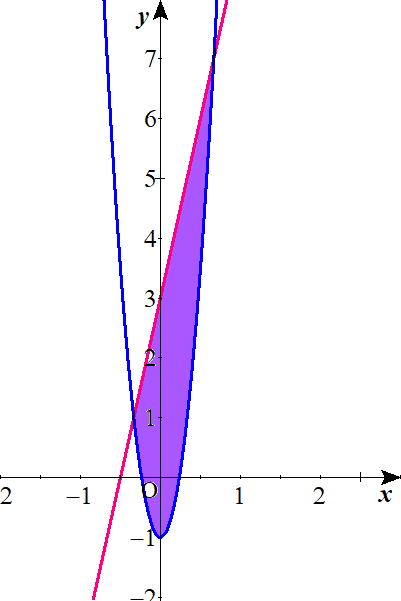
放物線と直線の交点を求めよう。
Lukia
今、（1）の問いでは、「点\(\mathrm{P}\)が動ける横の限界はどこか？」と聞いているわけです。
図を見てみると、放物線と直線の交点がその限界にあたるようです。
ということは、放物線と直線の交点を求めればよさそうですね。
$$\begin{align}18x^2-1=&6x+3 \\\\ 18x^2-6x-4=&0 \\\\ 9x^2-3x-2=&0\\\\ \left( 3x-2\right)\left( 3x+1\right)=&0\\\\ x=-\frac{1}{3} \ ,& \ x=\frac{2}{3} \end{align}$$
ゆえに
$$\begin{align}最大値:&\frac{2}{3} \ 最小値:&-\frac{1}{3}\end{align}$$
定数kをおいて考えよう。
ここで、放物線と直線の交点をそれぞれ
$$\begin{align}\mathrm{M}&\left( \frac{2}{3} \ , \ 7\right) \ m&\left( -\frac{1}{3} \ , \ 1\right) \quad \quad としておく.\end{align}$$
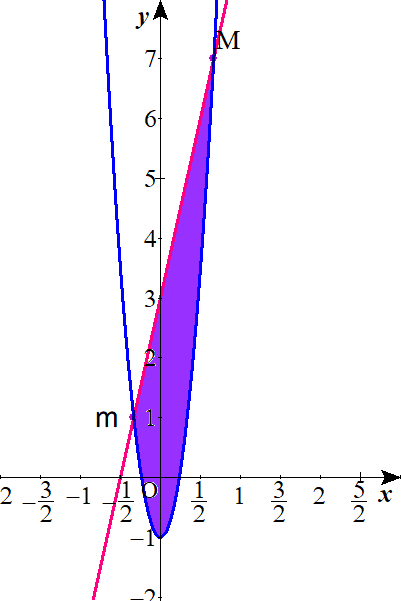
$$\begin{align}x-\frac{1}{18}y=&k\quad とする.\\\\ \left( kは \ k \geq 0 \ の実数と仮定する.\right) \\\\ 18x-y=&18k \\\\ y=&18x-18k\quad \quad \cdots*\end{align}$$
Lukia
透明なものさしとか、透明な下敷きなどがあれば、急な右肩上がりの直線を仮定して動かしてみてほしいのですが、
切片の\(-18k\)は、点\(m\)のとき最大で、点\(\mathrm{M}\)をとおるとき最小ということになります。
Lukia
\(-18k\)の最大値・最小値で考えてみましょう。
$$\begin{align}直線 \ y=18x-18k \ のy切片 \ -18k \ は\\\\ 点mをとおるとき最大\\\\点\mathrm{M}をとおるとき最小である\end{align}$$
$$\begin{align}1-18\times -\frac{1}{3}=&-18k \\\\ 7=&-18k \\\\ k=&-\frac{7}{18} \end{align}$$
$$\begin{align}7-18\times \frac{2}{3}=&-18k \\\\ -5=&-18k \\\\ k=&\frac{5}{18} \end{align}$$
以上より、
$$最大値\quad \frac{5}{18} \ , \ 最小値\quad -\frac{7}{18}$$
こたえ
(1)
$$\begin{align}最大値:\quad \frac{2}{3} \quad ,\quad 最小値:\quad -\frac{1}{3}\end{align}$$
(2)
$$最大値:\quad \frac{5}{18}\quad ,\quad 最小値:\quad -\frac{7}{18}$$
共有:
プロフィール
