高校数学の「接線の方程式・面積・回転体の体積」に関する問題を解いてみる。（Yahoo!知恵袋より）
[mathjax]
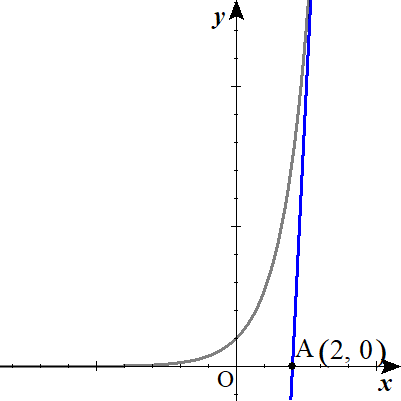
以下では、点\(\mathrm{A}\left( 2 \ , \ 0\right)\)から\(y=f\left( x\right)\)に引いた接線を\(l\)とする。
(1) 接線\(l\)の方程式を求めよ。
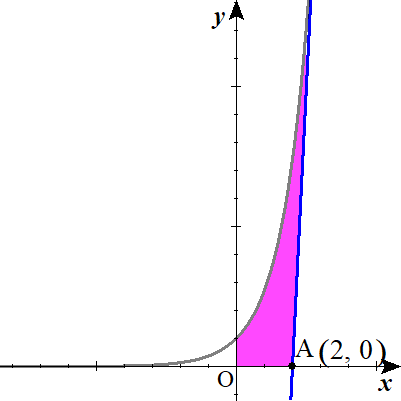
(2) \(y=f\left( x\right)\)のグラフと\(x\)軸、\(y\)軸、および接線\(l\)で囲まれた部分の面積\(\mathrm{S}\)を求めよ。
(3) (2)で求めた部分を\(x\)軸の周りに1回転させてできる回転体の体積\(\mathrm{V}\)を求めよ。
接線lの方程式を求める。
$$\begin{align}&接点を \ \left( t \ , \ e^t\right)\quad とする.\\\\ &接線lの方程式は \ y=e^t\left( x-t\right)+e^t \ とおける. \\\\&点\mathrm{A}の値を代入する.\\\\& 0=e^t\left( 2-t\right)+e^t\\\\ &e^t\cdot t=3e^t\\\\&e^t \neq 0\quad より両辺を \ e^t \ でわって,\\\\ &t=3\\\\ &y=e^3\left( x-3\right)+e^3\\\\& l:\quad y=e^3\left( x-2\right) \end{align}$$
面積Sを求める。
Lukia
回転体の体積を求める。
Lukia
バウムクーヘンは、曲線\(y=e^x\)に従い、さまざまな大きさの同心円となります。
うすっぺら～いバウムクーヘンでは、面積のままですが、バウムクーヘンを棒に突きさしていくことで、少しずつ厚みができ、体積となっていきます。
$$\begin{align}\frac{\mathrm{V}}{\pi}=&\int_{0}^{3} e^{2x} dx-e^6\int_{2}^{3} \left( x-2\right)^2 dx \\\\ ここで, \ 2x=&t \ とする. \\\\ 両辺を \ &x \ について微分する. \\\\ 2=&\frac{dt}{dx}\\\\ 2dx=&t\end{align}$$
$$\begin{align}\frac{\mathrm{V}}{\pi}=&\int_{0}^{6} e^t\cdot \frac{1}{2} dt-e^6\left[\frac{1}{3}x^3-2x^2+4x\right]_2^3 \\\\ =&\frac{1}{2}\left( e^6-1\right)-\frac{e^6}{3} \\\\ =&\frac{1}{6}\left( e^6-3\right)\ \\\\ \mathrm{V}=&\frac{\pi}{6}\left( e^6-3\right) \end{align}$$
こたえ
$$\begin{align}l:\quad y=&e^3\left( x-2\right) \\\\ \mathrm{S}=&\frac{1}{2}e^3-1\\\\ \mathrm{V}=&\frac{\pi}{6}\left( e^6-3\right) \end{align}$$
共有:
プロフィール
