Yahoo!知恵袋の高校数学カテゴリにあった「三角比と図形」に関する問題を解いてみる。
[mathjax]
\(\angle \mathrm{A}=45^{\circ} , \angle \mathrm{B}=60^{\circ} , b=5\sqrt{6}\)のとき、
辺の長さ a , c を求めよ。
解法
正弦定理を用いて。
Lukia
わかっている情報を書き込んでみましょう。
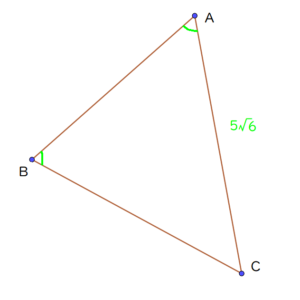
Lukia
正弦定理を用いて、\(\angle\mathrm{A}\)の対辺 \(a\) の大きさを求めます。
正弦定理より、
$$\begin{align}\frac{b}{\sin \angle\mathrm{B}}=&\frac{a}{\sin \angle \mathrm{A}} \\\\ & \\\\ a=&\frac{\sin \angle \mathrm{A}}{\sin \angle\mathrm{B}}\times b \\\\ =&\frac{\sqrt{2}}{2}\times \frac{2}{\sqrt{3}}\times 5\sqrt{6}\\\\ ゆえに& \\\\ \Large a=&10 \end{align}$$
余弦定理を用いて。
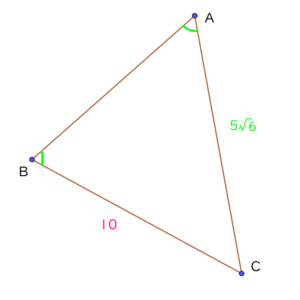
Lukia
そこで、余弦定理を用いて\(c\)の大きさを求めます。
Lukia
センター試験では、この形を覚えておいたほうがなにかと便利でした。
$$\Large \color{red}{\angle\mathrm{B} に関する余弦定理}$$
$$\Large\color{red}{\cos \angle\mathrm{B}=\frac{a^2+c^2-b^2}{2ac}} より、$$
$$\begin{align}\cos \angle\mathrm{B}=&\frac{10^2+c^2-\left( 5\sqrt{6}\right)^2}{2\cdot 10\cdot c} \\\\ \frac{1}{2}\times \left( 2\cdot 10\cdot c\right)=&25\times 4+c^2-25\times 6 \\\\ 10c=&c^2-50\\\\ c^2-10c=&50 \\\\ \left( c-5\right)^2-25=&50\\\\ \left( c-5\right)^2=&75 \\\\ c-5=& \pm 5\sqrt{3}\\\\ c=&5 \pm 5\sqrt{3} \end{align}$$
辺cの大きさは2つあっていいの？
Lukia
はたして両方とも こたえとしてよいのでしょうか。
ネックとなるのは、\(5\sqrt{3}\)の大きさですよね。
\(5+5\sqrt{3}\)は間違いなく \(c \gt 0\) を満たしていますが、
\(5-5\sqrt{3}\)は \(c \gt 0\) を満たしているのでしょうか。
ルート3≒1.7 として簡単に計算してみる。
Lukia
\(\sqrt{3} \sim 1.7\) と覚えておいてよいと思います。
$$\begin{align}5-5\sqrt{3}=&5\left( 1-\sqrt{3}\right) \\\\ =&5\left( 1-1.7\right) \\\\ =&-3.5\\\\ ただし、 c \gt 0 &より不適。 \end{align}$$
平方根に直して考える。
Lukia
もう少し複雑な数の大小比較であれば、平方根に直して考えるのが確実です。
$$\begin{align}5-5\sqrt{3}=&\sqrt{25}-\sqrt{75} \\\\ & \\\\ ここで、&\sqrt{25} \lt \sqrt{75} であるから、\\\\ & \\\\ 与式& \lt 0\\\\ & \\\\ ゆえに&不適。 \end{align}$$
マイナス5ルート3の数直線上の位置を考える。
Lukia
$$\begin{align}5\sqrt{3}=&\sqrt{75} より、\\\\ & \\\\ \sqrt{64} \lt 5&\sqrt{3} \lt \sqrt{81} であるから、\\\\ & \\\\ -\sqrt{81} \lt -5&\sqrt{3} \lt -\sqrt{64} \\\\ 5-9 \lt 5-5&\sqrt{3} \lt 5-8\\\\ -4 \lt 5-5&\sqrt{3} \lt -3\\\\ & \\\\ あきらかに\quad &5-5\sqrt{3} \lt 0 であるから、不適。 \end{align}$$
こたえ
$$\Large a=10$$
$$\Large c=5+5\sqrt{3}$$
共有:
プロフィール
