高校数学の「積分とその応用・絶対値を含む積分」に関する問題を解いてみる。（Yahoo!知恵袋より）
高校数学Ⅲ , 積分とその応用 , 絶対値を含む積分 , 数検準1級
問題
絶対値が含まれてるぞ！
ディノ
Lukia
ディノ
Lukia
ええっ、っていうか、そのアイス、私の・・・
ディノ
$$\begin{align}e^x=t とする。\quad \quad x=\log t でもある。 \end{align}$$
| $$x$$ | $$\quad 0 \ → \ 2\quad $$ |
| $$t$$ | $$\quad 1 \ → \ e^2\quad $$ |
$$\begin{align}両辺を&x \ で微分する。 \ e^x=&\frac{ \mathrm{ d } t }{ \mathrm{ d } x } \ tdx=&dt\ dx=&\frac{1}{t}dt\ ゆえに& \ 与式=&\int_{1}^{e^2} \vert t-3 \vert \cdot \frac{1}{t}dt \end{align}$$
Lukia
ああっ・・・私のアイスが・・・
ディノ
そのうちに溶けてもなんだし。（笑）
Lukia
うう、こうなったら、少しつきあってもらいますよっ。（涙）
絶対値をはずす。
Lukia
まず、どうしたらいいですか？
ディノ
\(y=\vert t-3 \vert\)のグラフを描く。
Lukia
ディノ
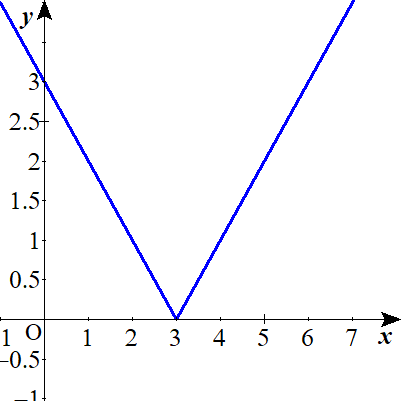
$$\begin{align}f\left( t\right)=&\left( t-3\right)\cdot \frac{1}{1} \quad \quad 3 \leq t \ のとき\ =&-\left( t-3\right)\cdot \frac{1}{1} \quad \quad 3 \gt t \ のとき\end{align}$$
Lukia
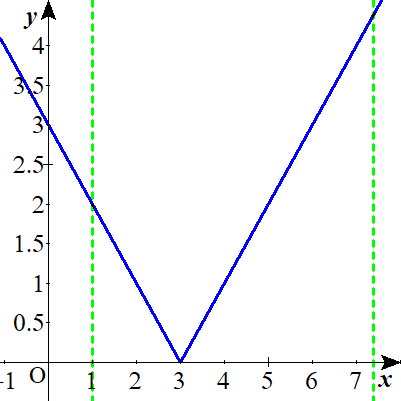
定義域みたいなものなのですが、上のグラフに\(1\)は簡単に打てるものの、\(e^2\)はぱっと思いつかないですね。
\(e\)はおよそ\(2.7\)なのですが、さて、\(3\)よりも右なのでしょうか、左にあるのでしょうか。
ディノ
小数点の計算するのはめんどくさいし・・・
！・・・
\(e \fallingdotseq 2.7 \fallingdotseq 3\)として、\(3^2=9\)だから、\(e^2\)は、\(3\)よりも右にある！
Lukia
もはや溶けるのを気にするべきアイスもないわけですから、もう少していねいにやってもらえません？
ディノ
じゃ、
\(\left( 2.7\right)^2=\left( 3-0.3\right)^2=9-1.8+0.09=7.29 \gt 3\)
はどうだ？
Lukia
でも結局、小数点を含んだ計算をしてしまってますよね。
ここまで丁寧なのはいらないんです。
もうちょっとぱっと考えられる方法はありませんか？
ディノ
あ、じゃ、こういうのはどうだ？
\(3=\left( \sqrt{3}\right)^2\)で・・・（チラッ）
おっ、いい感じなんだな。
\(\sqrt{3}\)そのものの大きさを考える。
\(1 \lt \sqrt{3} \lt 2\)で、\(e \fallingdotseq 2.7\) だから、
\(\sqrt{3} \lt e\)だ！
その大小関係は二乗したって変わんねーから、\(3 \lt e^2\)だ！
Lukia
で、ディノさんがあれこれ計算して出してくれたので、ちょっと正確な範囲をグラフに描きこんでおきましょうね。
積分の計算をしていく。
$$\begin{align}与式=&\int_{1}^{e^2} \vert t-3 \vert \cdot \frac{1}{t} dt
\ =&-\int_{1}^{3} \left( 1-\frac{3}{t}\right) dt+\int_{3}^{e^2} \left( 1-\frac{3}{t}\right) dt \end{align}$$
ディノ
Lukia
$$\begin{align}ここで、1-\frac{3}{t}=f\left( t\right) \ &とし、 \ f\left( t\right)の原関数を\mathrm{F}\left( t\right)&とする。 \ 与式=& -\mathrm{F}\left( 3\right)+\mathrm{F}\left( 1\right)+\mathrm{F}\left( e^2\right)-\mathrm{F}\left( 3\right)\ =&\mathrm{F}\left( e^2\right)-2\mathrm{F}\left( 3\right)+\mathrm{F}\left( 1\right) \end{align}$$
$$\begin{align}\mathrm{F}\left( t\right)=&t-3\log t+\mathrm{C}\quad \left( \mathrm{C}は積分定数\right) \ であるから、
\ 与式=&e^2-3\log e^2-2\left( 3-3\log 3\right)+1-3\log 1 \ =&e^2-6-6+6\log 3+1\ =&e^2-11+6\log 3 \end{align}$$
ディノ
Lukia
まぁ、場合によっては、\(6\log 3\)を\(\log 729\) とすることもできますが、ここらへんは解答の指示に従ってください。
・・・あれ？ディノさん？
ディノ
新しいの買ってきた。
Lukia
・・・えっ、ええ～～～？？？
ディノ
Lukia
こたえ
$$e^2-11+6\log 3$$
プロフィール
