高校数学の「絶対値を含む放物線と直線の共有点の個数」に関する問題を解いてみる。(Yahoo!知恵袋より)

2021年10月6日2023年1月11日二次関数実用数学技能検定（数学検定数検),数検2級,数検準2級

読了時間: 約1分50秒

Yahoo!知恵袋の高校数学カテゴリに掲載されていた「絶対値を含む放物線と直線の共有点の個数」に関する問題を解いてみました。

問題

$ \ k \ $は定数とする。
方程式 $ \ \vert x^2-x-2 \vert=2x+k \ $ の異なる実数解の個数を調べよ。

解法

$$\begin{align}f\left( x\right)=&\vert x^2-x-2 \vert-2x\quad とする。 \\\\ =&\vert \left( x+1\right)\left( x-2\right) \vert-2x \\\\ \\\\ f\left( x\right)=&x^2-3x-2\quad \left( x \lt -1, \ 2 \lt x\quad のとき\right)\\\\ f\left( x\right)=&-x^2-x+2\quad \left( -1 \leq x \leq 2\quad のとき\right) \end{align}$$
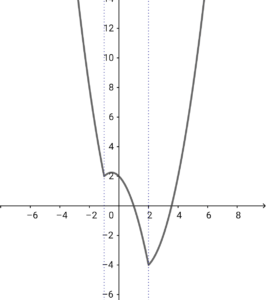
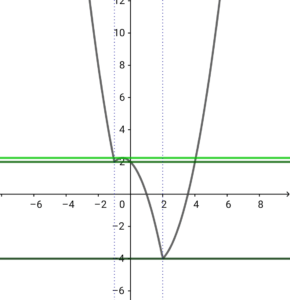
グラフは以下の通り。

以下、直線 $ \ y=k \ $ と $ \ f\left( x\right) \ $ との共有点の個数を求める。

① $ \ k \lt -4 \ $のとき実数解なし
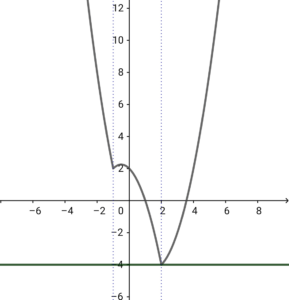
② $ \ k=-4 \ $のとき実数解 $ \ 1 \ $ 個

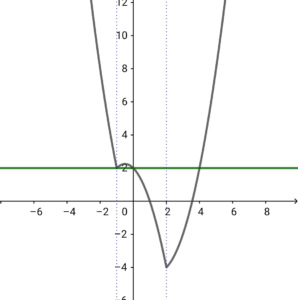③ $ \ -4 \lt k \lt 2 \ $のとき実数解 $ \ 2 \ $ 個
④ $ \ k=2 \ $のとき実数解 $ \ 3 \ $ 個

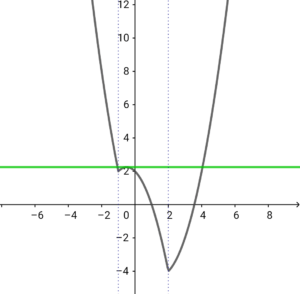
⑤ $ \ 2 \lt k \lt \ $$\Large \frac{9}{4}$のとき実数解 $ \ 4 \ $ 個
⑥ $ \ k= \ $$\Large \frac{9}{4}$のとき実数解 $ \ 3 \ $ 個
⑦ $ \ k \gt \ $$\Large \frac{9}{4}$のとき実数解 $ \ 2 \ $ 個

こたえ

① $ \ k \lt -4 \ $のとき実数解なし
② $ \ k=-4 \ $のとき実数解 $ \ 1 \ $ 個
③ $ \ -4 \lt k \lt 2 \ $のとき実数解 $ \ 2 \ $ 個
④ $ \ k=2 \ $のとき実数解 $ \ 3 \ $ 個
⑤ $ \ 2 \lt k \lt \ $$\Large \frac{9}{4}$のとき実数解 $ \ 4 \ $ 個
⑥ $ \ k= \ $$\Large \frac{9}{4}$のとき実数解 $ \ 3 \ $ 個
⑦ $ \ k \gt \ $$\Large \frac{9}{4}$のとき実数解 $ \ 2 \ $ 個

関連

プロフィール

Author Profile

Lukia_74

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。

カテゴリー