高校数学の「二次関数の頂点・値域」に関する問題を解いてみる。（Yahoo!知恵袋より）
[mathjax]
ただし、\(a\) , \(b\)は定数とする。
2つのグラフ \(y=f\left( x\right)\) , \(y=g\left( x\right)\)の頂点が一致するとき、
\(a\) ,\(b\)の値を求めよ。
また、\(0 \leq x \leq 3\)のとき、
\(f\left( x\right)\)の値域を求めよ。
二次関数は、とにっかく、平方完成して軸と頂点を意識。
Lukia
$$\begin{align}f\left( x\right)=&-2x^2+4x+3 \\\\ =&-2\left( x^2-2x\right)+3 \\\\ =&-2\left( x-1\right)^2+5 \end{align}$$
$$ゆえに、軸はx=1 , 頂点は\left( 1 , 5\right)$$
$$\begin{align}g\left( x\right)=&x^2-2ax+b \\\\ =&\left( x-a\right)^2-a^2+b \end{align}$$
$$ゆえに、軸はx=a , 頂点は\left( a\quad ,\quad -a^2+b\right)$$
Lukia
赤い放物線が\(\color{red}{g\left( x\right)}\)です。
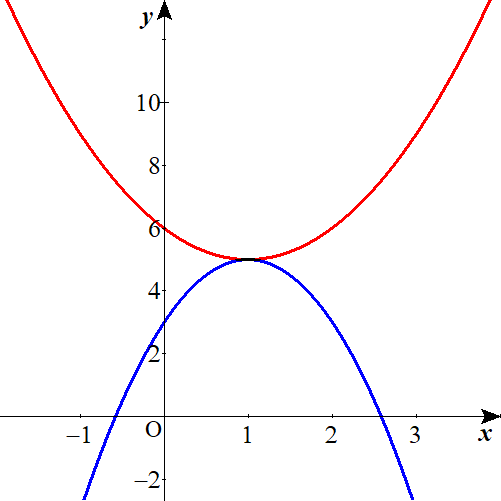
れもん
$$\begin{align}条件より、a=&1 \\\\ また、&\\\\ -a^2+b=&5 \\\\ b-1=&5\\\\ b=&6 \end{align}$$
$$以上より、a=1\quad,\quad b=6$$
フリーハンドでグラフを描けるようになろう。
Lukia
れもん
気を付けたほうがいいことってありますか？
Lukia
たとえば、\(y=6x^2\)なんてグラフですと、急激に大きくなってしまうので、\(x\)軸における幅\(1\)の目盛りと、\(y\)軸における幅\(1\)の目盛りを同じにしていたら、問題用紙の余白からはみ出してしまいます。
れもん
\(x=2\)のときは\(y=24\)なんて・・・
Lukia
\(e\)は、およそ\(2.7\)ぐらいなんですけど、これをまじめに考えていると大変なことになってしまいます。
つまり、\(x\)軸の目盛りの幅はなるべく正確なほうがよいのですが、\(y\)軸のほうはわりとアバウトでもいいのです。
さっきの\(y=6x^2\)のグラフの\(y\)軸の目盛りは、\(x\)軸のひと目盛りの幅に\(6\)の幅を割り当ててもいいってことです。
こういう臨機応変な対応ができるかどうかが、高校数学レベルだと必要になってくるわけですね。
れもん
Lukia
そして、今回は、軸の\(\color{#00ff00}{x=1}\)を緑の点線で示し、
定義域の右端にあたる\(\color{magenta}{x=3}\)をピンクの点線で示しています。
Lukia
れもん
軸の左側よりも、軸の右側の幅が広いですね。
Lukia
れもん
右の端点は・・・\(8\)も離れています！
Lukia
$$\begin{align}&f\left( x\right)は、\\\\ &軸がx=1 \ にある、上に凸の関数なので、 \\\\ &0 \leq x \leq 3において最大値はf\left( 1\right)のときであり、\\\\ &最小値は、軸より離れた端点f\left( 3\right)である。 \end{align}$$
求める値域は、
$$\begin{align}f\left( 3\right) \leq &y \leq f\left( 0\right) \\\\ すなわち、& \\\\ -3 \leq &y \leq 5 \end{align}$$
こたえ
$$\begin{align}a=1\quad,\quad b=6 \\\\ -3 \leq y \leq 5 \end{align}$$
共有:
プロフィール
