高校数学の「絶対値と不等式」に関する問題を解いてみる。（Yahoo!知恵袋より）
読了時間: 約1分42秒
[mathjax]
問題
\(x\)に関する不等式を解け。
\(\vert x+4 \vert \lt 3x\)
\(\vert x+4 \vert \lt 3x\)
解法
ディノ
おおっ！絶対値の問題だぞ！！
Lukia
ディノさん、やってみます？
ディノ
おう、やってみる！！
グラフ描けばいいんだったよな。
\(x\)が\(-4\)のときに\(x\)軸に交わって、\(-4\)よりも小さい範囲は、\(x\)軸で折り返されるんだよな。
グラフ描けばいいんだったよな。
\(x\)が\(-4\)のときに\(x\)軸に交わって、\(-4\)よりも小さい範囲は、\(x\)軸で折り返されるんだよな。
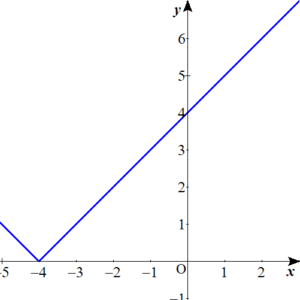
$$\begin{align}f\left( x\right)=&\vert x+4 \vert とすると
\\\\ x&+4 \left( -4\leq x\right)
\\\\ -x&-4 \left( x \lt -4\right)\end{align}$$
ディノ
描けたぞ！
Lukia
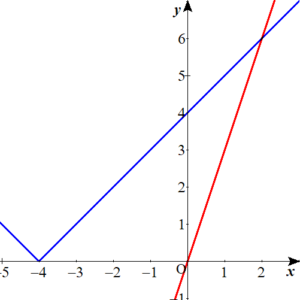
じゃ、次は\(y=3x\)も描き足してみましょう。
ディノ
こうだな。
Lukia
では、\(\color{red}{y=3x}\)が\(\color{blue}{y=\vert x+4 \vert}\)よりも上にあるのは、\(x\)がいくつのときですか。
ディノ
\(x+4 \lt 3x\) を解けばいいよな。
$$\begin{align}x+4 \lt &3x \\\\ 4 \lt &2x \\\\ 2 \lt &x \end{align}$$
Lukia
実際にグラフを見てみても、\(2 \lt x\)を満たしていますね。
こたえ
$$2 \lt x$$
ディナ
あら～、お勉強済んだかしら？
ディノ
おう、かーちゃん！一問解いたぞ！
ディナ
んま～、頼もしい！
センセ、ありがとうございますぅ～！
ささっ、おやつにしましょ。
センセ、ありがとうございますぅ～！
ささっ、おやつにしましょ。
Lukia
ディ、ディナさん？
解いたのはたった一問ですよ。
まだ、おやつには早いんじゃ・・・
解いたのはたった一問ですよ。
まだ、おやつには早いんじゃ・・・
ディナ
あらっ。
じゃ、食べたらまた勉強すればいいわよねぇ。
今日のおやつは柿ですよ～。
ビタミンCたっぷりで体にいいのよ～。
じゃ、食べたらまた勉強すればいいわよねぇ。
今日のおやつは柿ですよ～。
ビタミンCたっぷりで体にいいのよ～。
ディノ
そうだぞ、お肌にもいいぞ。
Lukia
（あああ、もう言ってるそばから食べてるし・・・）
じゃ、食べたら再開しましょうね。
じゃ、食べたら再開しましょうね。
すっごく嬉しそうに柿をもしゃもしゃ食べるディノさんなのでした。
共有:
プロフィール
Author Profile
