高校数学の「平面ベクトル(点の存在範囲)」に関する問題を解いてみる。(Yahoo!知恵袋より)

\( \ 0 \leq s+t \leq 3\quad ,\quad s \geq 0\quad ,\quad t \geq 0 \ \)を満たすとき、
点\( \ \mathrm{P} \ \)の存在範囲を図示せよ。
(2) \( \ \overrightarrow{\mathrm{OP}}=s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}} \ \)
\( \ 0 \leq s+t \leq \frac{1}{2}\quad ,\quad s \geq 0\quad ,\quad t \geq 0 \ \)を満たすとき、
点\( \ \mathrm{P} \ \)の存在範囲を図示せよ。
[mathjax]
(1)を解く。
$$\begin{align}&0 \leq s+t \leq 3\quad の各辺を\frac{1}{3}倍する. \\\\ &0 \leq \color{#f700ca}{\frac{1}{3}s}+\color{#f700ca}{\frac{1}{3}t} \leq 1\\\\ \\\\ \overrightarrow{\mathrm{OP}}=&s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}\\\\ =&3\cdot \color{#f700ca}{\frac{1}{3}s}\overrightarrow{\mathrm{OA}}+3\cdot \color{#f700ca}{\frac{1}{3}t}\overrightarrow{\mathrm{OB}} \\\\ =& \color{#f700ca}{\frac{1}{3}s}\cdot 3\overrightarrow{\mathrm{OA}}+\color{#f700ca}{\frac{1}{3}t}\cdot 3\overrightarrow{\mathrm{OB}} \end{align}$$
$$\begin{align}ここで,\quad &3\overrightarrow{\mathrm{OA}}=\overrightarrow{\mathrm{OA’}} \\\\ &3\overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{OB’}}\quad とする.\\\\ \\\\ また,\quad &\frac{1}{3}s=k\\\\ &\frac{1}{3}t=l\\\\ &\quad \left( k \ , \ l\quad は実数\right) \quad とすると, \end{align}$$
$$\begin{align}\overrightarrow{\mathrm{OP}}=&k\overrightarrow{\mathrm{OA’}}+l\overrightarrow{\mathrm{OB’}} \\\\ &\quad 0 \leq k+l \leq 1\quad ,\quad k \geq 0\quad ,\quad l \geq 0\quad となる. \end{align}$$
$$\begin{align}点\mathrm{P}の&存在範囲は, \\\\ &下図の \ \triangle \mathrm{OA’B’}\quad の周上とその内部.\end{align}$$
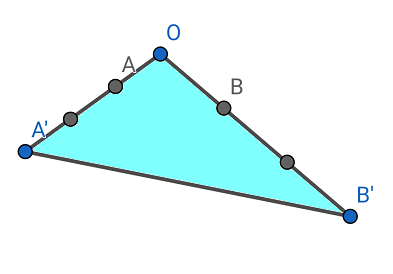
(2)を解く。
$$\begin{align}&0 \leq s+t \leq \frac{1}{2}\quad の各辺を2倍する. \\\\ &0 \leq \color{#f700ca}{2s}+\color{#f700ca}{2t} \leq 1\\\\ \\\\ \overrightarrow{\mathrm{OP}}=&s\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}\\\\ =&\frac{1}{2}\cdot \color{#f700ca}{2s}\overrightarrow{\mathrm{OA}}+\frac{1}{2}\cdot \color{#f700ca}{2t}\overrightarrow{\mathrm{OB}} \\\\ =& \color{#f700ca}{2s}\cdot \frac{1}{2}\overrightarrow{\mathrm{OA}}+\color{#f700ca}{2t}\cdot \frac{1}{2}\overrightarrow{\mathrm{OB}} \end{align}$$
$$\begin{align}ここで,\quad &\frac{1}{2}\overrightarrow{\mathrm{OA}}=\overrightarrow{\mathrm{OA’}} \\\\ &\frac{1}{2}\overrightarrow{\mathrm{OB}}=\overrightarrow{\mathrm{OB’}}\quad とする.\\\\ \\\\ また,\quad &2s=k\\\\ &2t=l\\\\ &\quad \left( k \ , \ l\quad は実数\right) \quad とすると, \end{align}$$
$$\begin{align}\overrightarrow{\mathrm{OP}}=&k\overrightarrow{\mathrm{OA’}}+l\overrightarrow{\mathrm{OB’}} \\\\ &\quad 0 \leq k+l \leq 1\quad ,\quad k \geq 0\quad ,\quad l \geq 0\quad となる. \end{align}$$
$$\begin{align}点\mathrm{P}の&存在範囲は, \\\\ &下図の \ \triangle \mathrm{OA’B’}\quad の周上とその内部.\end{align}$$
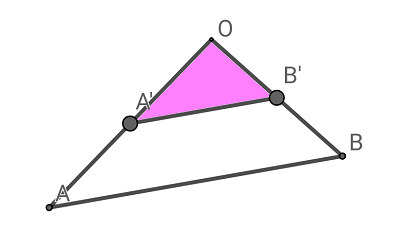
こたえ
(1)
$$点\mathrm{P}の存在範囲は, 下図の \ \triangle \mathrm{OA’B’}\quad の周上とその内部.$$

(2)
$$点\mathrm{P}の存在範囲は, 下図の \ \triangle \mathrm{OA’B’}\quad の周上とその内部.$$











ディスカッション
コメント一覧
まだ、コメントがありません