高校数学の「ヘロンの公式と内接円の半径」に関する問題を解いてみる。(Yahoo!知恵袋より)
読了時間: 約1分12秒
Yahoo!知恵袋の高校数学カテゴリに掲載されていた「ヘロンの公式と内接円の半径」に関する問題を解いてみました。
問題
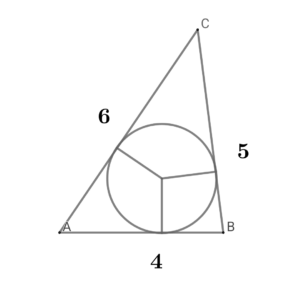
三角形\( \ \mathrm{ABC} \ \)について
\( \ a=4 \ \), \( \ b=5 \ \), \( \ c=6 \ \) のとき、内接円の半径を \( \ r \ \) とする。
三角形の面積 \( \ \mathrm{S} \ \) と、 \( \ r \ \) の値をそれぞれ求めよ。
\( \ a=4 \ \), \( \ b=5 \ \), \( \ c=6 \ \) のとき、内接円の半径を \( \ r \ \) とする。
三角形の面積 \( \ \mathrm{S} \ \) と、 \( \ r \ \) の値をそれぞれ求めよ。
解法
ヘロンの公式より$$\begin{align}\mathrm{S}=&\frac{1}{4}\sqrt{15\cdot \left( 10-5\right)\cdot \left( 9-6\right)\cdot \left( 11-4\right)} \\\\ =&\frac{1}{4}\sqrt{3\times 5\times 5\times 3\times 7} \\\\ =&\frac{15\sqrt{7}}{4} \ \cdots\quad ① \end{align}$$ 内心（内接円の中心）は、３つの頂角の二等分線の交点である。
また、内心から各辺に下ろした垂線の長さがその半径である。
$$\begin{align}\mathrm{S}=&\frac{1}{2}\cdot \left( a+b+c\right)r \\\\ =&\frac{15}{2}r \ \cdots\quad ② \end{align}$$ ①, ② より
$$\begin{align}\frac{15}{2}r=&\frac{15\sqrt{7}}{4} \\\\ r=&\frac{\sqrt{7}}{2} \end{align}$$
こたえ
$$\frac{\sqrt{7}}{2}$$
共有:
プロフィール
Author Profile
