高校数学の「絶対値絡みの文字式とその値」に関する問題を解いてみる。(Yahoo!知恵袋より)
読了時間: 約0分49秒
Yahoo!知恵袋の高校数学カテゴリに掲載されていた「絶対値絡みの文字式とその値」に関する問題を解いてみました。
問題
\( \ a=3+\sqrt{15} \ \)
\( \ b=\vert a^2-7a \vert \ \) のとき
\(\Large \frac{a}{b}\)の値を求めよ。
\( \ b=\vert a^2-7a \vert \ \) のとき
\(\Large \frac{a}{b}\)の値を求めよ。
解法
\( \ b=\vert a^2-7a \vert \ \) のグラフは以下の通り。
\( \ 3 \lt \sqrt{15} \lt 4 \ \)
\( \ 6 \lt 3+\sqrt{15} \lt 7 \ \)
\( \ 6 \lt a \lt 7 \ \) より
\( \ b=-a^2+7a \ \) である。
$$\begin{align}\frac{a}{b}=&\frac{a}{-a^2+7a} \\\\ =&\frac{1}{-a+7} \\\\ =&\frac{1}{4-\sqrt{15}}\\\\ =&\frac{4+\sqrt{15}}{16-15} \\\\ =&4+\sqrt{15} \end{align}$$
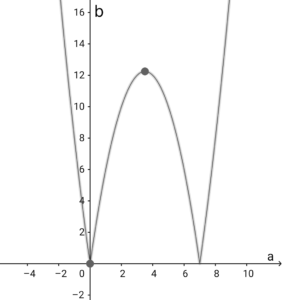\( \ 3 \lt \sqrt{15} \lt 4 \ \)\( \ 6 \lt 3+\sqrt{15} \lt 7 \ \)
\( \ 6 \lt a \lt 7 \ \) より
\( \ b=-a^2+7a \ \) である。
$$\begin{align}\frac{a}{b}=&\frac{a}{-a^2+7a} \\\\ =&\frac{1}{-a+7} \\\\ =&\frac{1}{4-\sqrt{15}}\\\\ =&\frac{4+\sqrt{15}}{16-15} \\\\ =&4+\sqrt{15} \end{align}$$
こたえ
\(\Large 4+\sqrt{15}\)
共有:
プロフィール
Author Profile
