高校数学の「正弦定理・余弦定理・四面体の体積」に関する問題を解いてみる。(Yahoo!知恵袋より)
読了時間: 約5分58秒
Yahoo!知恵袋の高校数学カテゴリに掲載されていた「正弦定理・余弦定理・四面体の体積」に関する問題を解いてみました。
問題
\( \ \triangle \mathrm{ABC} \ \)において、 \( \ \mathrm{AB}=5 \ \)、 \( \ \mathrm{AC}=7 \ \)、\( \ \cos \angle \mathrm{BAC}= \ \)\(\Large \frac{1}{7}\)である。
（1）辺\( \ \mathrm{BC} \ \)の長さを求めよ。
（2）平面上\( \ \mathrm{ABC} \ \)にない点\( \ \mathrm{D} \ \)をとり、四面体\( \ \mathrm{ABCD} \ \)をつくる。
\( \ \sin \angle \mathrm{ADC}= \ \)\(\Large \frac{\sqrt{21}}{7}\)、 \( \ \cos \angle \mathrm{CAD}=- \ \)\(\Large \frac{1}{7}\)のとき、
辺\( \ \mathrm{CD} \ \)および辺\( \ \mathrm{AD} \ \)の長さを求めよ。
（3）(2)において、\( \ \mathrm{BC}=\mathrm{BD} \ \)であるとき、
四面体\( \ \mathrm{ABCD} \ \)の体積を求めよ。
（1）辺\( \ \mathrm{BC} \ \)の長さを求めよ。
（2）平面上\( \ \mathrm{ABC} \ \)にない点\( \ \mathrm{D} \ \)をとり、四面体\( \ \mathrm{ABCD} \ \)をつくる。
\( \ \sin \angle \mathrm{ADC}= \ \)\(\Large \frac{\sqrt{21}}{7}\)、 \( \ \cos \angle \mathrm{CAD}=- \ \)\(\Large \frac{1}{7}\)のとき、
辺\( \ \mathrm{CD} \ \)および辺\( \ \mathrm{AD} \ \)の長さを求めよ。
（3）(2)において、\( \ \mathrm{BC}=\mathrm{BD} \ \)であるとき、
四面体\( \ \mathrm{ABCD} \ \)の体積を求めよ。
解法(1)・(2)
(1)を解く。(余弦定理で辺の大きさを求める）
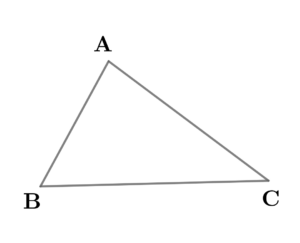\( \ \mathrm{BC}=a \ \)とする。 ただし、\( \ a \gt 0 \ \) である。また、\( \ \mathrm{AC}=b=7 \ \), \( \ \mathrm{AB}=c=5 \ \) とする。
余弦定理より
$$\begin{align}\cos \angle \mathrm{BAC}=&\frac{b^2+c^2-a^2}{2\cdot bc} \\\\ \frac{1}{7}=&\frac{49+25-a^2}{2\cdot 7\cdot 5} \\\\ 10=&-a^2+74\\\\ a^2=&64\\\\ a \gt &0\quad より\\\\ a=&8 \end{align}$$
(2)を解く。(正弦定理・余弦定理で辺の大きさを求める）
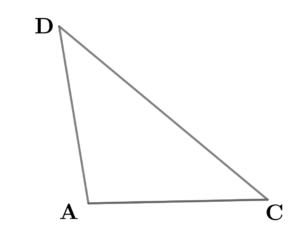$$\begin{align}\sin \angle \mathrm{CAD}=&\sqrt{1-\left( \cos \angle \mathrm{CAD}\right)^2} \\\\ =&\sqrt{1-\frac{1}{49}} \\\\ =&\frac{4\sqrt{3}}{7} \end{align}$$ 正弦定理より$$\begin{align}\frac{\mathrm{AC}}{\sin \angle \mathrm{ADC}}=&\frac{\mathrm{CD}}{\sin \angle \mathrm{CAD}} \\\\ \mathrm{CD}=&7\cdot \frac{4\sqrt{3}}{7}\cdot \frac{7}{\sqrt{21}} \\\\ =&4\sqrt{7} \end{align}$$
余弦定理より
$$\begin{align}\cos \angle \mathrm{CAD}=&\frac{\mathrm{AD}^2+\mathrm{AC}^2-\mathrm{CD}^2}{2\cdot \mathrm{AD}\cdot \mathrm{AC}} \\\\ -\frac{1}{7}=&\frac{\mathrm{AD}^2+49-16\times 7}{2\cdot \mathrm{AD}\cdot 7} \\\\ -2\mathrm{AD}=&\mathrm{AD}^2+7\left( 7-16\right) \end{align}$$ $$\begin{align}\mathrm{AD}^2+2\mathrm{AD}-7\times 9=&0 \\\\ \left( \mathrm{AD}+9\right)\left( \mathrm{AD}-7\right)=&0 \\\\ \mathrm{AD} \gt &0\quad より\\\\ \mathrm{AD}=&7 \end{align}$$
解法（3）
四面体の底面となる三角形を決める
四面体 \( \ \mathrm{ABCD} \ \) の体積を \( \ \mathrm{V} \ \) とする。
これを求めるにあたり、底面を \( \ \triangle \mathrm{ACD} \ \) とし、
頂点 \( \ \mathrm{B} \ \) から底面におろした垂線の長さを高さとする。
いま、\( \ \triangle \mathrm{BCD} \ \)と\( \ \triangle \mathrm{ACD} \ \)はそれぞれ\( \ \mathrm{BC}=\mathrm{BD} \ \) , \( \ \mathrm{AC}=\mathrm{AD} \ \) の二等辺三角形である。
二等辺三角形の頂角の二等分線は、その底辺を垂直に二等分する。
\( \ \angle \mathrm{DBC} \ \)の二等分線と辺\( \ \mathrm{CD} \ \)の交点を\( \ \mathrm{M} \ \)とする。
$$\begin{align}\mathrm{BM}=&\sqrt{\mathrm{BC}^2-\mathrm{CM}^2} \\\\ =&\sqrt{64-28} \\\\ =&6 \end{align}$$ \( \ \angle \mathrm{DAC} \ \)の二等分線と辺\( \ \mathrm{CD} \ \)の交点を\( \ \mathrm{M} \ \)とする。
$$\begin{align}\mathrm{AM}=&\sqrt{\mathrm{AC}^2-\mathrm{CM}^2} \\\\ =&\sqrt{49-28} \\\\ =&\sqrt{21} \end{align}$$
\( \ \triangle \mathrm{ABM} \ \)において点 \( \ \mathrm{B} \ \) から辺 \( \ \mathrm{AM} \ \) におろした垂線の足を点 \( \ \mathrm{H} \ \) とする。
\( \ \triangle \mathrm{ABM} \ \)の面積を\( \ \mathrm{S} \ \)とする。
ヘロンの公式より
$$\begin{align}\mathrm{S}=&\frac{1}{4}\sqrt{\left( 5+6+\sqrt{21}\right)\left( 5+6-\sqrt{21}\right)\left( 6+\sqrt{21}-5\right)\left( \sqrt{21}+5-6\right)} \\\\ =&\frac{1}{4}\sqrt{\left( 11+\sqrt{21}\right)\left( 11-\sqrt{21}\right)\left( \sqrt{21}+1\right)\left( \sqrt{21}-1\right)} \\\\ =&\frac{1}{4}\sqrt{\left( 121-21\right)\left( 21-1\right)}\\\\ =&\frac{1}{4}\cdot 10\cdot 2\sqrt{5}\\\\ =&5\sqrt{5} \end{align}$$ また
$$\begin{align}\mathrm{S}=\frac{1}{2}\mathrm{AM}\cdot \mathrm{BH}&\quad より \\\\ \frac{1}{2}\mathrm{AM}\cdot \mathrm{BH}=&5\sqrt{5} \\\\ \mathrm{BH}=&\frac{10\sqrt{5}}{\sqrt{21}} \end{align}$$
$$\begin{align}\mathrm{V}=&\frac{1}{3}\mathrm{S}_{\triangle \mathrm{ACD}}\cdot \mathrm{BH} \\\\ =&\frac{1}{3}\times \frac{1}{2}\times 7\times 4\sqrt{7}\times \frac{\sqrt{21}}{7}\times \frac{10\sqrt{5}}{\sqrt{21}} \\\\ =&\frac{20\sqrt{35}}{3} \end{align}$$
これを求めるにあたり、底面を \( \ \triangle \mathrm{ACD} \ \) とし、
頂点 \( \ \mathrm{B} \ \) から底面におろした垂線の長さを高さとする。
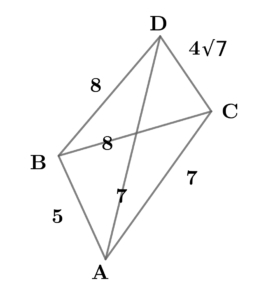
いま、\( \ \triangle \mathrm{BCD} \ \)と\( \ \triangle \mathrm{ACD} \ \)はそれぞれ\( \ \mathrm{BC}=\mathrm{BD} \ \) , \( \ \mathrm{AC}=\mathrm{AD} \ \) の二等辺三角形である。
二等辺三角形の頂角の二等分線は、その底辺を垂直に二等分する。
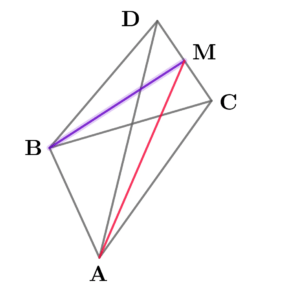
\( \ \angle \mathrm{DBC} \ \)の二等分線と辺\( \ \mathrm{CD} \ \)の交点を\( \ \mathrm{M} \ \)とする。
$$\begin{align}\mathrm{BM}=&\sqrt{\mathrm{BC}^2-\mathrm{CM}^2} \\\\ =&\sqrt{64-28} \\\\ =&6 \end{align}$$ \( \ \angle \mathrm{DAC} \ \)の二等分線と辺\( \ \mathrm{CD} \ \)の交点を\( \ \mathrm{M} \ \)とする。
$$\begin{align}\mathrm{AM}=&\sqrt{\mathrm{AC}^2-\mathrm{CM}^2} \\\\ =&\sqrt{49-28} \\\\ =&\sqrt{21} \end{align}$$
\( \ \triangle \mathrm{ABM} \ \)において点 \( \ \mathrm{B} \ \) から辺 \( \ \mathrm{AM} \ \) におろした垂線の足を点 \( \ \mathrm{H} \ \) とする。
\( \ \triangle \mathrm{ABM} \ \)の面積を\( \ \mathrm{S} \ \)とする。
ヘロンの公式より
$$\begin{align}\mathrm{S}=&\frac{1}{4}\sqrt{\left( 5+6+\sqrt{21}\right)\left( 5+6-\sqrt{21}\right)\left( 6+\sqrt{21}-5\right)\left( \sqrt{21}+5-6\right)} \\\\ =&\frac{1}{4}\sqrt{\left( 11+\sqrt{21}\right)\left( 11-\sqrt{21}\right)\left( \sqrt{21}+1\right)\left( \sqrt{21}-1\right)} \\\\ =&\frac{1}{4}\sqrt{\left( 121-21\right)\left( 21-1\right)}\\\\ =&\frac{1}{4}\cdot 10\cdot 2\sqrt{5}\\\\ =&5\sqrt{5} \end{align}$$ また
$$\begin{align}\mathrm{S}=\frac{1}{2}\mathrm{AM}\cdot \mathrm{BH}&\quad より \\\\ \frac{1}{2}\mathrm{AM}\cdot \mathrm{BH}=&5\sqrt{5} \\\\ \mathrm{BH}=&\frac{10\sqrt{5}}{\sqrt{21}} \end{align}$$
かなり計算が大変ですね。
高校数学の場合、最終的にはシンプルな値になることがほとんどなので、
それを想定して、あえて有理化をしていません。
高校数学の場合、最終的にはシンプルな値になることがほとんどなので、
それを想定して、あえて有理化をしていません。
また、ヘロンの公式は、カスタマイズしたものを用いました。
https://makelemonadejp.com/customize-herons-formula$$\begin{align}\mathrm{V}=&\frac{1}{3}\mathrm{S}_{\triangle \mathrm{ACD}}\cdot \mathrm{BH} \\\\ =&\frac{1}{3}\times \frac{1}{2}\times 7\times 4\sqrt{7}\times \frac{\sqrt{21}}{7}\times \frac{10\sqrt{5}}{\sqrt{21}} \\\\ =&\frac{20\sqrt{35}}{3} \end{align}$$
こたえ
$$\begin{align}\mathrm{BC}=&8 \\\\ \mathrm{CD}=&4\sqrt{7} \\\\ \mathrm{AD}=&7\\\\ \mathrm{V}=&\frac{20\sqrt{35}}{3} \end{align}$$共有:
プロフィール
Author Profile