高校数学の「二次関数の最大値・最小値」に関する問題を解いてみる。(Yahoo!知恵袋より)

[mathjax]
(1) \( \ m\left( a\right) \ \)を\( \ a \ \)で表せ。
(2) \( \ \mathrm{M}\left( a\right) \ \)を\( \ a \ \)で表せ。
(3) 関数\( \ b=m\left( a\right) \ \)および\( \ b=\mathrm{M}\left( a\right) \ \)のグラフを\( \ ab \ \)平面にそれぞれ図示せよ。
軸と定義域の位置関係から「最小値」を判断する。

Lukia
定義域がなかったら、間違いなく\( \ f(1) \ \)が最小値となります。
しかし、今回の問題では、定義域が設定されているので、そう簡単にはコトは運びません。
というわけで、軸と定義域の位置関係から、最小値を導きだしてみます。

Lukia
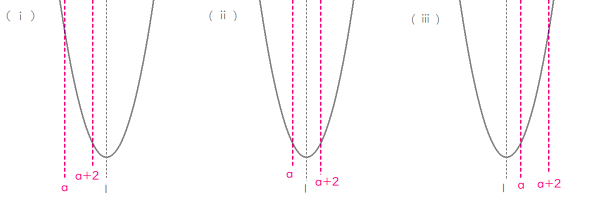
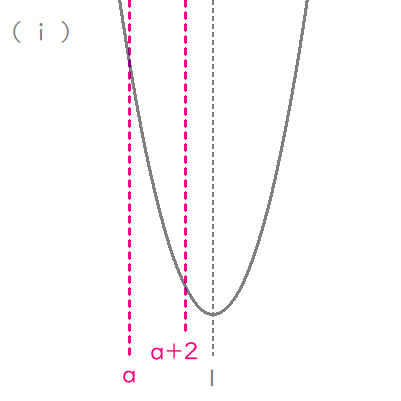
$$\begin{align}\left( ⅰ\right)\quad \quad a+2 \lt 1& \ すなわち\quad a \lt -1\quad のとき \\\\ m\left( a\right)=&f\left( a+2\right)\\\\ =&a^2+2a+3 \end{align}$$
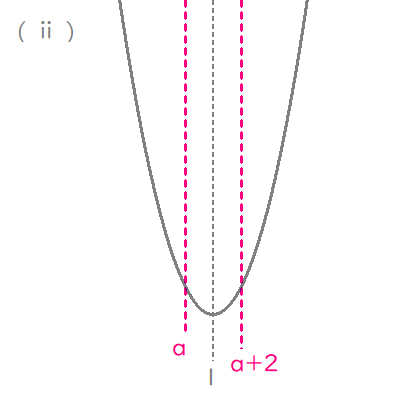
$$\begin{align}\left( ⅱ\right)\quad \quad a \lt 1 \lt a+2& \ すなわち\quad -1 \lt a \lt 1\quad のとき \\\\ m\left( a\right)=&f\left( 1\right) \\\\ =&2 \end{align}$$
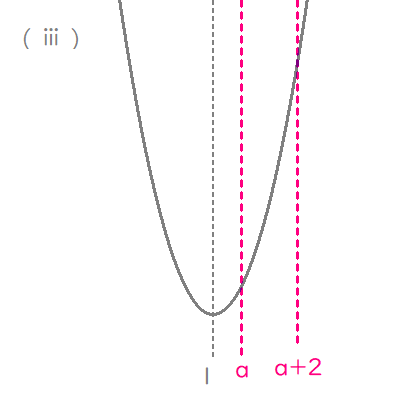
$$\begin{align}\left( ⅲ\right)\quad \quad 1 \lt a& \ のとき \\\\ m\left( a\right)=&f\left( a\right) \\\\ =&a^2-2a+3 \end{align}$$
「最大値」は、軸と定義域の中央との位置関係で判断しよう。

Lukia
最大値は、「定義域の中央」すなわち今回は、\( \ x=a+1 \ \)と軸との位置関係で判断できるんでしたね。
軸から遠い端点が最大値を取ります。

Lukia
定義域を三兄弟にたとえてみようと思います。
ちなみに、以下の三兄弟、なんと数式でできています。
数学のグラフ描画ソフト「GRAPES」で描きました。
「定義域」家の三兄弟(下に凸バージョン)


Lukia
定義域家では、兄弟の並ぶ順番はいつも固定されており、左から一郎・次郎・三郎が並ぶことになっています。
三人の間は等間隔となっています。

Lukia
下に凸の放物線の場合で示します。
わかりやすいように、三兄弟の口が下に凸となっていますね。
一郎・次郎 軸 三郎


Lukia
まず、軸によって、一郎・次郎の2人と、三郎のひとりに分けられたとします。
次郎が常に軸に近いところにいるのは、いうまでもないと思いますが、
軸と一郎、または軸と三郎で比べると、一郎のほうが次郎がいるぶん、軸との距離がありますよね。
というわけで、最大値を取るのは「一郎」ということになります。

れもん

Lukia
私は、最大値のことだけ言えばいいことになりますね。
それでは、次に進みます。
一郎 軸 次郎・三郎


Lukia
すると、軸と一郎との距離に比べて、軸と三郎の距離のほうが遠くなっていますね。だって、三郎からすれば、軸の前に次郎がいますからね。
というわけで、最大値をとるのは、「三郎」ということになります。

れもん
定義域家の三兄弟の間に軸が存在する間は、軸(すなわち頂点)が最小値をとりますね。
軸=次郎


Lukia
もともと、一郎と次郎、または三郎と次郎の間は等間隔なのですが、軸が次郎と重なったことで、軸と一郎、軸と三郎の距離も等間隔になってしまいました。

Lukia

れもん

Lukia
軸 三兄弟

Lukia


Lukia
今回は、一郎が最も軸に近いですね。
三兄弟は等間隔に並んでいるのですから、軸から最も遠い位置にいるのは、「三郎」ということになります。
ゆえに最大値をとるのは、「三郎」ということになります。

れもん
最小値は、軸にもっとも近い「一郎」がとることになります。
三兄弟 軸

Lukia
三兄弟の右側に軸がある。というパターンもやっておきましょう。


Lukia
というわけで、最大値をとるのは、「一郎」ということになります。

れもん
問題に戻って。



$$\begin{align}a+1 \leq 1\quad & \ すなわち \ a \leq 0\quad のとき \\\\ \mathrm{M}\left( a\right)=&f\left( a\right)=a^2-2a+3 \end{align}$$



$$\begin{align}a+1 \geq 1\quad & \ すなわち \ a \geq 0 \ のとき \\\\ \mathrm{M}\left( a\right)=&f\left( a+2\right)\\\\ =&a^2+2a+3 \end{align}$$
(3)
$$m\left( a\right)\quad のグラフは以下のとおり。$$
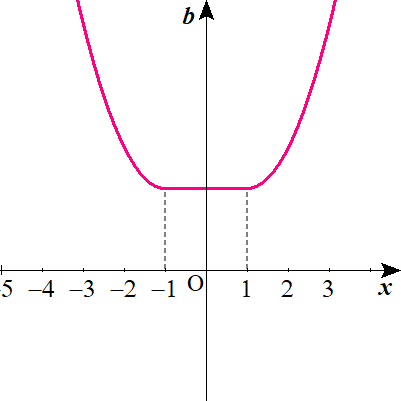
$$\mathrm{M}\left( a\right)\quad のグラフは以下のとおり。$$
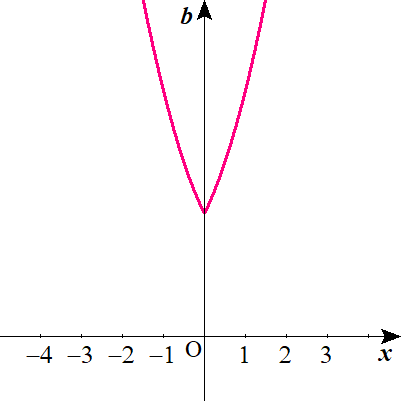
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません