Yahoo!知恵袋の高校数学カテゴリにあった、ドモアブルの定理を使う計算問題をやってみた。

2018年9月21日2023年1月15日複素数平面実用数学技能検定（数学検定 数検),数検準1級

解法

Lukia

ひとまず、分母を有理化してみます。

$$\begin{align}\left( \frac{\sqrt{2}}{\sqrt{3}+i}\right)^8=&\left( \frac{\sqrt{2}\left( \sqrt{3}-i\right)}{\left( \sqrt{3}+i\right)\left( \sqrt{3}-i\right)}\right)^8 \\\\ =&\left( \frac{\sqrt{2}}{4}\left( \sqrt{3}-i\right)\right)^8 \\\\ =&\left( \frac{\sqrt{2}}{4}\cdot 2\right)^8\left( \cos \left( \color{blue}{2\pi}-\frac{ \pi }{ 6 }\right)+i\sin \left( \color{blue}{2\pi}-\frac{ \pi }{ 6 }\right)\right)^8 \end{align}$$

Lukia

ここで、指数の計算をしてしまいましょう。
　\(\left( \frac{\sqrt{2}}{4}\cdot 2\right)^8\)
\(=\left( 2^\left( \frac{1}{2}-2+1\right)\right)^8\)
\(=\left( 2^\left( -\frac{1}{2}\right)\right)^8\)
\(=2^\left( -\frac{1}{2}\times 8\right)=2^\left( -4\right)=\frac{1}{16}\)

Lukia

また、\(-\frac{ \pi }{ 6 }\)　がイメージしにくい、計算しにくい方は、
\(\color{blue}{2\pi}+\theta\)の形で考えてみましょう。
\(\color{blue}{2\pi}\)って、結局0のことだから、つけておいても問題ありませんね。
何倍しても0ですし。

Lukia

ただし、ドモアブルの定理を使うまでは、
\(\color{blue}{2\pi}-\frac{ \pi }{ 6 }\) のままでおいておきましょう。
計算して、\({\frac{ 11 }{ 6 }}\pi\)　としてしまうと、
あとの計算がややこしくなって、ミスのもとになってしまいます。

$$\begin{align}与式=&\frac{1}{16}\lbrace \cos \left( \color{blue}{2\pi}-\frac{ \pi }{ 6 }\right)+i\sin \left( \color{blue}{2\pi}-\frac{ \pi }{ 6 }\right)\rbrace^8 \\\\ =&\frac{1}{16}\lbrace \cos \left( \color{blue}{2\pi}-{\frac{ 4 }{ 3 }}\pi\right)+i\sin \left( \color{blue}{2\pi}-{\frac{ 4 }{ 3 }}\pi\right)\rbrace \\\\ =&\frac{1}{16}\left( \cos {\frac{ 2 }{ 3 }}\pi+i\sin {\frac{ 2 }{ 3 }}\pi\right) \end{align}$$

Lukia

\(\cos {\frac{ 2 }{ 3 }}\pi\) や\(\sin {\frac{ 2 }{ 3 }}\pi\)の値を考えるのは、
数学Ⅲをやるようなレベルの方には問題ないことですよね。

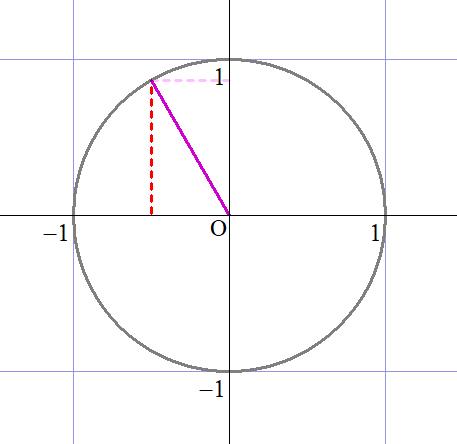
$$\begin{align}\frac{1}{16}\left( \cos {\frac{ 2 }{ 3 }}\pi+i\sin {\frac{ 2 }{ 3 }}\pi\right) =&\frac{1}{16}\left( \frac{1}{2}+\frac{\sqrt{3}}{2}i\right) \\\\ =&\frac{1}{16}\cdot \frac{1}{2}\left( 1+\sqrt{3}i\right) \\\\ =&\frac{1+\sqrt{3}i}{32} \end{align}$$

こたえ

$$\Large \left( \frac{\sqrt{2}}{\sqrt{3}+i}\right)^8=\frac{1+\sqrt{3}i}{32} $$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。