高校数学の「三角形の内角を求める【余弦定理・正弦定理】」に関する問題を解いてみる。(Yahoo!知恵袋より)
読了時間: 約2分30秒
問題
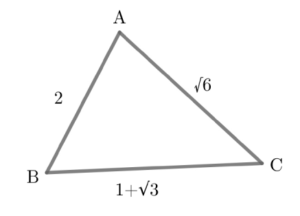[mathjax]左図のような三角形ABCがあるとき、
三つの内角の大きさをそれぞれ求めよ。
余弦定理より
$$\begin{align}\cos \mathrm{C}=&\frac{\mathrm{BC}^2+\mathrm{CA}^2-\mathrm{AB}^2}{2\cdot \mathrm{BC}\cdot \mathrm{CA}} \\\\ =&\frac{\left( 1+\sqrt{3}\right)^2+\sqrt{6}^2-2^2}{2\cdot \left( 1+\sqrt{3}\right)\cdot \sqrt{6}} \\\\ =&\frac{\left( \sqrt{3}+3\right)\color{#0004fc}{\left( \sqrt{3}-1\right)}}{\sqrt{6}\left( \sqrt{3}+1\right)\color{#0004fc}{\left( \sqrt{3}-1\right)}}\\\\ =&\frac{2\sqrt{3}}{2\sqrt{6}}\\\\ =&\frac{1}{\sqrt{2}} \end{align}$$
$$\angle \mathrm{C}=45^{\circ}$$
正弦定理より
$$\begin{align}\frac{\sin \mathrm{B}}{\sqrt{6}}=&\frac{\sin 45^{\circ}}{2} \\\\ \sin \mathrm{B}=&\frac{1}{2}\times \frac{1}{\sqrt{2}}\times\sqrt{6} \\\\ =&\frac{\sqrt{3}}{2} \end{align}$$
$$\begin{align}\frac{\sin \mathrm{B}}{\sqrt{6}}=&\frac{\sin 45^{\circ}}{2} \\\\ \sin \mathrm{B}=&\frac{1}{2}\times \frac{1}{\sqrt{2}}\times\sqrt{6} \\\\ =&\frac{\sqrt{3}}{2} \end{align}$$
ここで、辺\( \ \mathrm{BC}\ \)と辺\( \ \mathrm{CA}\ \)の大小比較をする。
$$\begin{align}\sqrt{3}+1 \gt &\sqrt{6}\quad と仮定する。\\\\ 両辺をそれぞれ二乗すると \\\\ 左辺=&4+2\sqrt{3}\\\\ 右辺=&6 \end{align}$$
$$\begin{align}左辺について\\\\ 1 \lt &\sqrt{3} \lt 2\\\\ 2 \lt &2\sqrt{3} \lt 4\\\\ 6 \lt &4+2\sqrt{3} \lt 8\end{align}$$
$$\begin{align}ゆえに \\\\ \sqrt{3}+1 \gt &\sqrt{6} \end{align}$$
$$\begin{align}\sqrt{3}+1 \gt &\sqrt{6}\quad と仮定する。\\\\ 両辺をそれぞれ二乗すると \\\\ 左辺=&4+2\sqrt{3}\\\\ 右辺=&6 \end{align}$$
$$\begin{align}左辺について\\\\ 1 \lt &\sqrt{3} \lt 2\\\\ 2 \lt &2\sqrt{3} \lt 4\\\\ 6 \lt &4+2\sqrt{3} \lt 8\end{align}$$
$$\begin{align}ゆえに \\\\ \sqrt{3}+1 \gt &\sqrt{6} \end{align}$$
辺\( \ \mathrm{BC}\ \)が最大辺であるといえるので、
\( \ \angle \mathrm{B}=60^{\circ}\ \)
三角形の内角の和は\( \ 180^{\circ}\ \)であるから、
\( \ \angle \mathrm{A}=180^{\circ}-\left( 45^{\circ}+60^{\circ}\right)=75^{\circ}\ \)
三辺の大きさが与えられているので、余弦定理→正弦定理と用いていけば、角度自体は簡単に求まります。
しかし、それだけでは、記述式解答では100点はもらえません。
サインの場合、鋭角鈍角ともに正の値を取るため、辺の大小比較をして、最大辺の確定をしなければならないのです。
共有:
プロフィール
Author Profile