高校数学の「指数・対数の大小関係」に関する問題を解いてみる。（Yahoo!知恵袋より）
読了時間: 約2分48秒
[mathjax]
問題
次の5つの数の大小関係を調べ、左から小さい順に並び替えよ。
\( \ \sqrt[3]{4} \ , \ 1 \ , \ 16^{\frac{1}{5}} \ , \ \log_{4}3 \ , \ \log_{5}3 \ \)
\( \ \sqrt[3]{4} \ , \ 1 \ , \ 16^{\frac{1}{5}} \ , \ \log_{4}3 \ , \ \log_{5}3 \ \)
まずはふたつのグループに分けて考えよう。
Lukia
5つの数は大きく指数グループと対数グループに分けられますね。
並び替えるのですから、指数または対数に統一できればいいのですが、対数の底が統一されていないので、対数で統一することはちょっと難しそうです。
かといって、対数のほうを2を底とする指数に直すことも難しそう。
こういう場合、あんまり無理はせず、まずは分けやすいグループ内で大小関係を明らかにし、グループの大小を考えることにしてみましょう。
並び替えるのですから、指数または対数に統一できればいいのですが、対数の底が統一されていないので、対数で統一することはちょっと難しそうです。
かといって、対数のほうを2を底とする指数に直すことも難しそう。
こういう場合、あんまり無理はせず、まずは分けやすいグループ内で大小関係を明らかにし、グループの大小を考えることにしてみましょう。
Lukia
ちなみに、
\( \ \sqrt[3]{4} \ , \ 1 \ , \ 16^{\frac{1}{5}} \ \)を「前半グループ」とし、
\( \ \log_{4}3 \ , \ \log_{5}3 \ \)を「後半グループ」とします。
\( \ \sqrt[3]{4} \ , \ 1 \ , \ 16^{\frac{1}{5}} \ \)を「前半グループ」とし、
\( \ \log_{4}3 \ , \ \log_{5}3 \ \)を「後半グループ」とします。
「前半グループ」内の大小関係を明らかにする。
Lukia
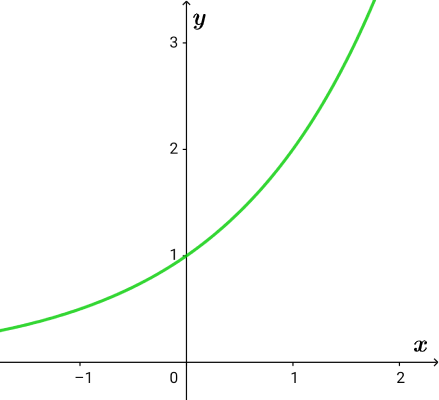
以下に示すグラフは、
\( \ y=2^x \ \)です。
「前半のグループ」はこの緑色の曲線上に存在します。
\( \ y=2^x \ \)です。
「前半のグループ」はこの緑色の曲線上に存在します。
$$\begin{align}\sqrt[3]{4}&\quad ,\quad 1\quad ,\quad 16^{\frac{1}{5}}\quad は2を底とすると \\\\ 2^{\frac{2}{3}}&\quad ,\quad 2^0\quad ,\quad 2^{\frac{4}{5}}\quad と表せる. \\\\ さらに&指数の分母を15にすると\\\\ 2^{\frac{10}{15}}&\quad ,\quad 2^{\frac{0}{15}}\quad ,\quad 2^{\frac{12}{15}}\quad となる。\\\\ 以上より&\quad 1 \lt \sqrt[3]{4} \lt 16^{\frac{1}{5}} \end{align}$$
「後半のグループ」内の大小関係を明らかにする。
Lukia
ふたつの対数の底は、それぞれ\( \ 4 \ \)と\( \ 5 \ \)です。ふたつの対数は\( \ 1 \ \)と比べて大きいのか小さいのか、考えてみましょう。
Lukia
\( \ y=\log_{4}x \ \)が\( \ 1 \ \)となるのは、\( \ x=4 \ \)のとき。
また、\( \ y=\log_{5}x \ \)が\( \ 1 \ \)となるのは、\( \ x=5 \ \)のとき。
また、\( \ y=\log_{5}x \ \)が\( \ 1 \ \)となるのは、\( \ x=5 \ \)のとき。
Lukia
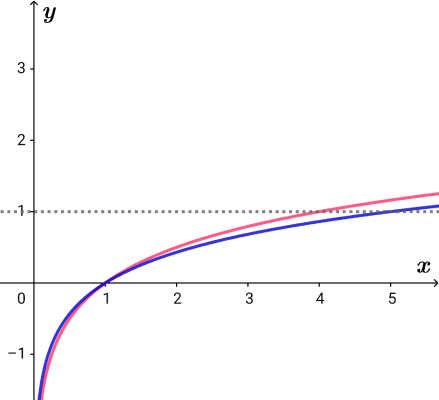
さらに、ふたつの対数の真数はいずれも\( \ 3 \ \)ですね。以下にグラフを示しますが、\( \ y=1 \ \)となるまでに、\( \ \log_{4}x \ \)のほうは、\( \ x \ \)が\( \ 4 \ \)となればいいのに、
\( \ \log_{5}x \ \)のほうは、\( \ x \ \)が\( \ 5 \ \)になってやっと到達します。
つまり、底を\( \ a \ \)とすると、\( \ 1 \lt a \ \)のとき、
\( \ \log_{a}x \ \)のグラフは\( \ a \ \)の値が大きくなればなるほど、なかなか\( \ y=1 \ \)に到達できず、
\( \ x \ \)軸に近い、ひらべ〜ったいグラフとなります。
\( \ \log_{5}x \ \)のほうは、\( \ x \ \)が\( \ 5 \ \)になってやっと到達します。
つまり、底を\( \ a \ \)とすると、\( \ 1 \lt a \ \)のとき、
\( \ \log_{a}x \ \)のグラフは\( \ a \ \)の値が大きくなればなるほど、なかなか\( \ y=1 \ \)に到達できず、
\( \ x \ \)軸に近い、ひらべ〜ったいグラフとなります。
Lukia
ということは、「後半のグループ」内の大小関係は
\( \ \log_{5}3 \lt \log_{4}3 \ \)となります。
\( \ \log_{5}3 \lt \log_{4}3 \ \)となります。
いよいよふたつのグループを統一する。
$$\begin{align}\log_{4}3& \lt 1\quad より \\\\ 5つの数の&大小関係は \\\\ \log_{5}3& \lt \log_{4}3 \lt 1 \lt \sqrt[3]{4} \lt 16^{\frac{1}{5}} \end{align}$$
こたえ
$$\log_{5}3 \lt \log_{4}3 \lt 1 \lt \sqrt[3]{4} \lt 16^{\frac{1}{5}} $$
共有:
プロフィール
Author Profile
