高校数学の「三次関数の『最大値』を求める（極値じゃないよ！）」に関する問題を解いてみる。（Yahoo!知恵袋より）

2019年4月4日2023年1月14日微分と積分実用数学技能検定（数学検定 数検),数検2級,数検準1級

Lukia

まずは\( \ f\left( x\right) \ \)のグラフがどんな形なのかを知るため、微分してみましょう。

$$\begin{align}f’\left( x\right)=&3x^2-8x+4 \\\\\ f’\left( x\right)=0& \ を \ xに関する二次方程式とみなして解く. \\\\\ f’\left( x\right)=&\left( x-2\right)\left( 3x-2\right)=0\\\\\ &x=2 \ , \ x=\frac{2}{3} \end{align}$$

さらに微分して「変曲点」を求める.
$$\begin{align}f"\left( x\right)=&6x-8 \ \\\\ f"\left( x\right)=&0\quad となるのは \\\\\ x=&\frac{4}{3}\quad のとき. \end{align}$$
増減表は以下の通り.

$$x$$	$$0$$		$$\frac{2}{3}$$		$$\frac{4}{3}$$		$$2$$	$$\cdots$$
$$f’\left( x\right)$$	$$+$$		$$0$$	$$-$$			$$0$$	$$+$$
$$f"\left( x\right)$$	$$-$$				$$0$$	$$+$$
$$f\left( x\right)$$	$$0$$		$$\frac{32}{27}$$		$$\frac{16}{27}$$		$$0$$

増減表をもとづいたグラフの概形は以下の通り.

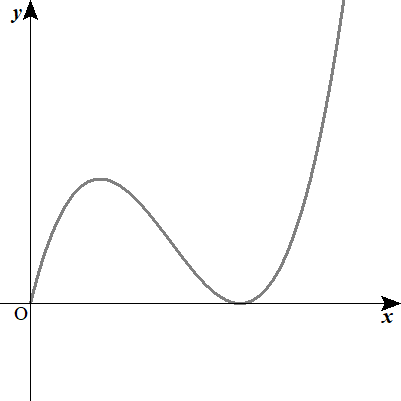
三次関数は変曲点に関して対称

極値をもつ三次関数は、もとの関数を2回微分して得られる「変曲点」に関して対称です。
そして、変曲点について2：1または1：2の位置に、極値と同じ値をとるx座標があります。

場合分けをして最大値を求める

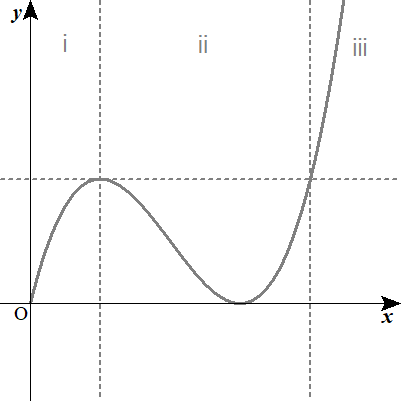
$$\begin{align}ⅰ)\quad &0 \lt a \lt \frac{2}{3}\quad のとき \\\\ \ &f\left( a\right)=a^3-4a^2+4a\quad が最大値.\\\\ ⅱ)\quad & \frac{2}{3} \leq a \leq \frac{8}{3}\quad のとき \\\\ \ &f\left( \frac{2}{3}\right)\quad またはf\left( \frac{8}{3}\right)\quad のときの\quad \frac{32}{27}が最大値.\\\\ \ ⅲ)\quad &\frac{8}{3} \lt a \quad のとき \\\\ &f\left( a\right)=a^3-4a^2+4a\quad が最大値.\end{align}$$

こたえ

$$\begin{align}ⅰ)\quad &0 \lt a \lt \frac{2}{3}\quad のとき \ \ \\\\ &f\left( a\right)=a^3-4a^2+4a\quad が最大値.\ \\\\ ⅱ)\quad & \frac{2}{3} \leq a \leq \frac{8}{3}\quad のとき \ \\\\ \ &f\left( \frac{2}{3}\right)\quad またはf\left( \frac{8}{3}\right)\quad のときの\quad \frac{32}{27}が最大値.\ \\\\ \ ⅲ)\quad &\frac{8}{3} \lt a \quad のとき \ \\\\ \ &f\left( a\right)=a^3-4a^2+4a\quad が最大値.\end{align}$$

プロフィール

Author Profile

元・再受験生、元塾講師、元高校非常勤講師。広島育ち。
中・高国語の教員免許を取得するも、塾講師時代は英語や数学ばかり教えていた。
思うところあって大学再受験を決意。理転し、数学Ⅲ、化学、生物を独習する。国立大学へ合格するも、2018年3月に再受験生生活にピリオドを打つ。
モットーは「自分の予定はキャンセルできても、生徒の予定はキャンセルできない」と「主婦（夫）こそ理系たれ」。
広島のお好み焼きとグレープフルーツが大好き。どっちかというと左党。楽しみはひとりカラオケ。
高校で教鞭を取った経験から、現在は「現代文」と「小論文」の指導力アップを目指し、自己研鑽中。最近は趣味として高校数学を解く。