高校数学の「二項定理」に関する問題を解いてみる。（Yahoo!知恵袋より）
読了時間: 約1分1秒
[mathjax]
問題
(1) \( \ \left( x^2+\frac{1}{x}\right)^{10} \ \)について\( \ x^{11} \ \)項の係数を求めよ.
(2) \( \ \left( 2x^4-\frac{1}{x}\right)^{10} \ \)について定数項の係数を求めよ.
(1)
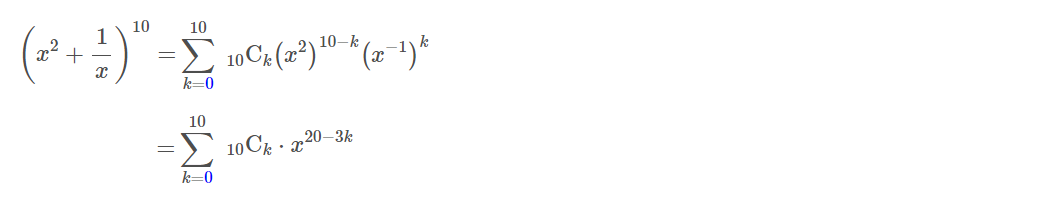
各項は,
で求められる.
$$\begin{align}11=&20-3r \ 3r=&9 \\\\ r=&3 \end{align}$$
$${}_{10} \mathrm{C}_3=\frac{10\cdot 9\cdot 8}{3\cdot 2\cdot 1}=120$$
(2)
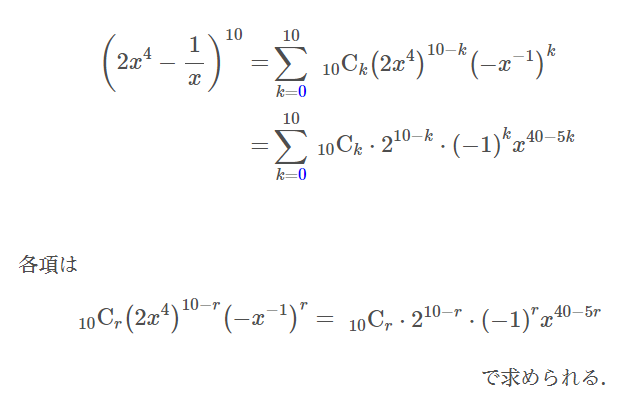
$$\begin{align}定数項の次数は&0 \ であるから, \\\\ 40-5r=&0 \\\\ r=&8 \end{align}$$
$$\begin{align}{}_{10} \mathrm{C}_8\cdot 2^{10-8}\cdot \left( -1\right)^8\cdot x^{40-40}=&\frac{10\cdot 9}{2\cdot 1}\cdot 2^2\cdot x^0 \\\\ =&180 \end{align}$$
こたえ
$$\begin{align}\left( 1\right)\quad &120 \\\\ \left( 2\right)\quad &180 \end{align}$$
共有:
プロフィール
Author Profile
