高校数学の「方程式の解の個数」に関する問題を解いてみる。（Yahoo!知恵袋より）

2019年1月30日2023年1月14日数と式実用数学技能検定（数学検定数検),数検準2級

読了時間: 約4分22秒

[mathjax]

問題

方程式$ \ \vert 2\vert x-1 \vert +x-2 \vert -k=0 \ $が異なる4つの実数解をもつための$ \ k \ $の値の範囲は,$ \ \color{#0004fc}{ア} \lt k \lt \color{#0004fc}{イ} \ $である。

グラフが描けなきゃはじまらない。

Lukia

方程式と書いてあるので、ついつい式変形でなんとかなりそうな気がしますが、絶対値がらみの問題の場合、グラフに描くなどの視覚化せずに解答を作成するのは難しいと思います。

Lukia

絶対値の問題を見たら、$ \ xy \ $平面上に描かれたグラフを$ \ x \ $軸でパタンと折り返し、すべて第1象限と第2象限上に集約させる。というイメージを持っておいてください。

$$\begin{align}\vert 2\vert x-1 \vert +x-2 \vert -k=&0\quad より \\\\ \ y=f\left( x\right)=&\vert 2\vert x-1 \vert +x-2 \vert\quad\cdots\cdots\quad ① と \\\\ y=&k\quad\cdots\cdots\quad ② に分けて考える. \end{align}$$

Lukia

まずは、ざっくりと内側の絶対値をはずしていきます。

①において
$$\begin{align}&\left( 1 \leq x\quad のとき\right) \\\\ f\left( x\right)=&\vert 2\left( x-1\right)+x-2 \vert\\\\ =&\vert 3x-4 \vert\quad \cdots\cdots\quad ③\\\\ \ &\left( x \lt 1\quad のとき\right)\\\\ f\left( x\right)=&\vert 2\cdot -\left( x-1\right)+x-2 \vert\\\\ =&\vert -x \vert\quad\cdots\cdots\quad ④ \end{align}$$

Lukia

①の式が③と④に分かれました。
さらにそれぞれ細かく考えていけば、グラフが描けます。

③において
$$\begin{align}f\left( x\right)=&3x-4\quad \left( \frac{4}{3}\leq x\quad のとき\right)\quad \cdots\cdots\quad ⑤\\\\ \ f\left( x\right)=&-\left( 3x-4\right)\quad \left( 1 \leq x \lt \frac{4}{3}\quad のとき\right)\quad \cdots\cdots\quad ⑥ \end{align}$$
④において
$$\begin{align}f\left( x\right)=&-x\quad \left( x \leq 0\quad のとき\right)\quad \cdots\cdots\quad ⑦ \\\\ \ f\left( x\right)=&x\quad \left( 0 \lt x \lt 1\quad のとき\right)\quad \cdots\cdots\quad ⑧ \end{align}$$
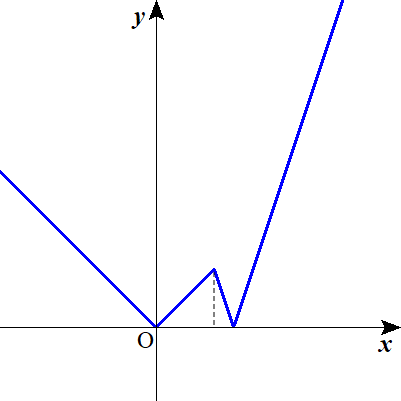
⑤ , ⑥ , ⑦ , ⑧をもとに描いたグラフは以下の通り.

Lukia

いかがですか。こんなグラフを数式だけで解くのは相当難しそうですよね。
逆に、出題者は、細かく場合分けをして、4本の直線が引けるかどうかを試しています。
つまり、「アナタ、絶対値のグラフ描けますか？」って聞いているってことですね。

定数kをひとりぼっちにした理由。

Lukia

最初に式変形をして、左辺にあった定数$ \ k \ $を右辺に移項し、
①と②の式に分けました。
なぜ、わざわざ$ \ k \ $だけをひとりぼっちにしたのかというと、
$ \ x \ $軸に平行な$ \ y=k \ $とすることで、
①のグラフとの共有点の個数を判別しやすくするため。です。

Lukia

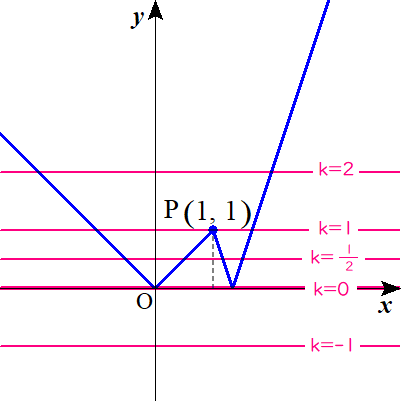
式⑥と式⑧の交点を$ \ \mathrm{P}\left( \ 1 \ , \ 1 \ \right) \ $とします。
さらに,直線$ \ y=k \ $を$ \ k=2 \ , \ 1 \ , \ \frac{1}{2} \ , \ 0 \ , \ -1 \ $を例に引いてみます。

Lukia

青い直線と、ピンクの直線の交点が共有点となります。
グラフの上から,
$ \ k=2\quad のとき\quad 2個 \ $
$ \ k=1\quad のとき\quad 3個 \ $
$ \ k=\frac{1}{2}\quad のとき\quad 4個 \ $
$ \ k=0\quad のとき\quad 2個 \ $
$ \ k=-1\quad のとき\quad 0個 \ $　となっていますね。

Lukia

つまり、$ \ y=k \ $が$ \ y=0 \ $と$ \ y=1 \ $の間にあれば、共有点が4個存在するということになります。

$$\begin{align}y=k\quad は, \ &x \ 軸に平行な直線である. \\\\ グラフより,&y=f\left( x\right) \ と \ y=k \ が4つの異なる共有点をもつのは, \\\\ &0 \lt k \lt 1\quad のとき \end{align}$$