高校数学の「動き回る放物線の軸と固定された定義域」に関する問題を解いてみる。【Yahoo!知恵袋より】
読了時間: 約2分3秒
Yahoo!知恵袋の高校数学カテゴリに掲載されていた「動き回る放物線の軸と固定された定義域」に関する問題を解いてみました。
問題
\( \ a \ \)は定数とする。関数\( \ y=3x^2-6ax+2 \ \) \( \ \left( 0 \leqq x \leqq 2\right) \ \)について、以下の問いに答えよ。
1) 最大値を求めよ。
2）最小値を求めよ。
1) 最大値を求めよ。
2）最小値を求めよ。
解法
\( \ y=f\left( x\right) \ \) とする。
$$\begin{align}f\left( x\right)=&3\left( x^2-2ax\right)+2 \\\\ =&3\left( x-a\right)^2-3a^2+2 \end{align}$$
軸と定義域の位置関係で、以下の5通りに場合分けできる。
 |
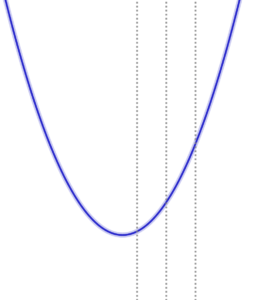1) \( \ a \leqq 0 \ \) のとき 最大値 \( \ f\left( 2\right)=14-12a \ \) 最小値 \( \ f\left( 0\right)=2 \ \) |
 |
2)\( \ 0 \lt a \lt 1 \ \) のとき 最大値 \( \ f\left( 2\right)=14-12a \ \) 最小値 \( \ f\left( a\right)=-3a^2+2 \ \) |
 |
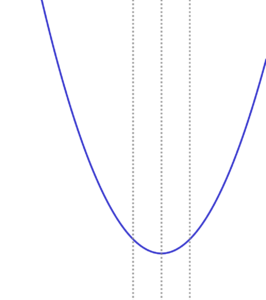3)\( \ a=1 \ \) のとき 最大値 \( \ f\left( 2\right)=f\left( 0\right)=2 \ \) 最小値 \( \ f\left( a\right)=f\left( 1\right)=-1 \ \) |
 |
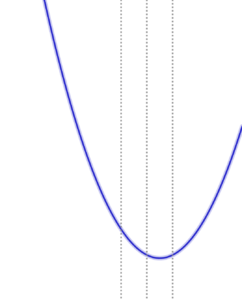4)\( \ 1 \lt a \lt 2 \ \) のとき 最大値 \( \ f\left( 0\right)=2 \ \) 最小値 \( \ f\left( a\right)=-3a^2+2 \ \) |
 |
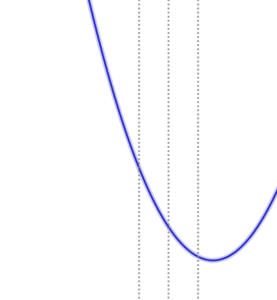5)\( \ 2 \leqq a \ \) のとき 最大値 \( \ f\left( 0\right)=2 \ \) 最小値 \( \ f\left( 2\right)=14-12a \ \) |
こたえ
| 1) 最大値 | \( \ a \leqq 1 \ \) のとき \( \ f\left( 2\right)=14-12a \ \) |
| \( \ 1 \lt a \ \) のとき \( \ f\left( 0\right)=2 \ \) |
|
| 2)最小値 | \( \ a \leqq 0 \ \) のとき \( \ f\left( 0\right)=2 \ \) |
| \( \ 0 \lt a \lt 1 \ \) または \( \ 1 \lt a \lt 2 \ \) のとき \( \ f\left( a\right)=-3a^2+2 \ \) |
|
| \( \ a=1 \ \) のとき \( \ f\left( a\right)=f\left( 1\right)=-1 \ \) |
|
| \( \ 2 \leqq a \ \) のとき \( \ f\left( 2\right)=14-12a \ \) |
共有:
プロフィール
Author Profile
