高校数学の「三角関数の条件を満たすθの範囲を求める」問題を解いてみる。【Yahoo!知恵袋より】
読了時間: 約1分39秒
Yahoo!知恵袋の高校数学カテゴリに掲載されていた「三角関数の条件を満たすθの範囲を求める」問題を解いてみました。
問題
\( \ 0 \leqq \theta \lt 2\pi \ \) のとき、
\( \ \left( \cos \theta+1\right)\left( 2\sin \theta-\sqrt{3}\right) \geqq 0 \ \) を満たす\( \ \theta \ \)を求めよ。
\( \ \left( \cos \theta+1\right)\left( 2\sin \theta-\sqrt{3}\right) \geqq 0 \ \) を満たす\( \ \theta \ \)を求めよ。
解法
与式を満たすのは、1) \( \ \cos \theta +1 \geqq 0 \ \) かつ \( \ 2\sin \theta-\sqrt{3} \geqq 0 \ \)
すなわち、\( \ \cos \theta \geqq -1 \ \) かつ \( \ \sin \theta \geqq \displaystyle\frac{\sqrt{3}}{2} \ \) のときか、
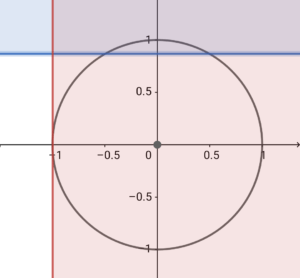
上の図で、赤と青の塗りつぶしが合わさって紫がかっているところがありますね。
それと単位円が重なっている部分が条件を満たす\( \ \theta \ \)の範囲となります。
それと単位円が重なっている部分が条件を満たす\( \ \theta \ \)の範囲となります。
2) \( \ \cos \theta +1 \geqq 0 \ \) かつ \( \ 2\sin \theta-\sqrt{3} \geqq 0 \ \)
すなわち、\( \ \cos \theta \lt -1 \ \) かつ \( \ \sin \theta \lt \displaystyle\frac{\sqrt{3}}{2} \ \) のとき。
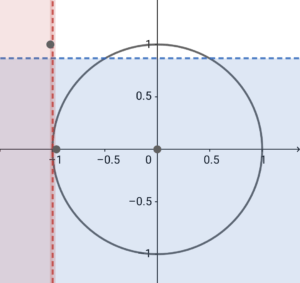
ただし、\( \ \cos \theta \lt -1 \ \) は存在しないので、(2)は不適。
\( \ \cos \theta \ \)の存在範囲（？）は\( \ -1 \leqq \cos \theta \leqq 1 \ \)です。
赤で塗りつぶし領域が、単位円の外側にありますね。
青の領域は単位円と重なっている部分もあるけれど、赤の領域は全く重なっていないので、これは「不適」（条件を満たさない）となります。
赤で塗りつぶし領域が、単位円の外側にありますね。
青の領域は単位円と重なっている部分もあるけれど、赤の領域は全く重なっていないので、これは「不適」（条件を満たさない）となります。
\( \ \displaystyle\frac{\pi}{3} \leqq \theta \leqq \displaystyle\frac{2}{3}\pi \ \)
こたえ
\( \ \displaystyle\frac{\pi}{3} \leqq \theta \leqq \displaystyle\frac{2}{3}\pi \ \)共有:
プロフィール
Author Profile