高校数学の「線形計画法」に関する問題を解いてみる。【Yahoo!知恵袋より】
読了時間: 約2分27秒
Yahoo!知恵袋の高校数学カテゴリに掲載されていた「線形計画法」に関する問題を解いてみました。
問題
2種類の薬品\( \ \mathrm{P},\mathrm{Q} \ \)がある。
その\( \ 1 \ \)gについて、\( \ \mathrm{A} \ \)成分、\( \ \mathrm{B} \ \)成分の量と価格は、以下の表の通りである。
その\( \ 1 \ \)gについて、\( \ \mathrm{A} \ \)成分、\( \ \mathrm{B} \ \)成分の量と価格は、以下の表の通りである。
| \( \ \mathrm{A} \ \)成分 | \( \ \mathrm{B} \ \)成分 | 価格 | |
| \( \ \mathrm{P} \ \) | \( \ 2 \ \)mg | \( \ 1 \ \)mg | \( \ 4 \ \)円 |
| \( \ \mathrm{Q} \ \) | \( \ 1 \ \)mg | \( \ 2 \ \)mg | \( \ 6 \ \)円 |
\( \ \mathrm{A} \ \)を\( \ 12 \ \)mg以上、\( \ \mathrm{B} \ \)を\( \ 15 \ \)mg以上とる必要があるとき、その総価格を最小にするには、\( \ \mathrm{P},\mathrm{Q} \ \)をそれぞれ何gずつとればよいか。
解法
\( \ \mathrm{P} \ \)を\( \ x \ \)g、\( \ \mathrm{Q} \ \)を\( \ y \ \)g とるとする。\( \ \mathrm{A} \ \)成分は、
\( \ \displaystyle\frac{2}{1000}x+\displaystyle\frac{1}{1000}y \geqq \displaystyle\frac{12}{1000} \ \)
\( \ \mathrm{B} \ \)成分は、
\( \ \displaystyle\frac{1}{1000}x+\displaystyle\frac{2}{1000}y \geqq \displaystyle\frac{15}{1000} \ \)
と表せるので、
求める薬品は、以下の連立不等式を満たす必要がある。
\begin{eqnarray} \left\{ \begin{array}{l} 2x + y \geqq 12 \\ x + 2y \geqq 15 \end{array} \right. \end{eqnarray} この連立不等式を満たす領域は以下の図の青く塗りつぶされた部分である。（境界を含む）
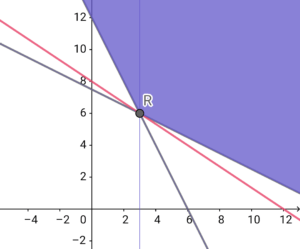
特に点\( \ \mathrm{R} \ \)の座標は\( \ \left( 3 \ , \ 6\right) \ \)である。
総価格を\( \ \mathrm{C} \ \)とすると、
\( \ \mathrm{C}=4x+6y \ \)と表せる。
\( \ y \ \)について解き、\( \ l \ \) とする。(上の図の赤い直線）
\( \ y=-\displaystyle\frac{2}{3}x+\displaystyle\frac{\mathrm{C}}{6} \ \)
総価格が最小になるのは、直線\( \ l \ \) が点\( \ \mathrm{R} \ \) を通るとき。
ゆえに、求める総価格は、\( \ 48 \ \)円である。
\( \ y=-\displaystyle\frac{2}{3}x+\displaystyle\frac{\mathrm{C}}{6} \ \)の切片である
\( \ \displaystyle\frac{\mathrm{C}}{6} \ \) は、直線が点\( \ \mathrm{R} \ \)を通るときに最小値を取ります。 ものさしでこの直線と平行な線を青い領域にずらしてみてください。切片はどんどん上に存在するようになるはずです。
\( \ \displaystyle\frac{\mathrm{C}}{6} \ \) は、直線が点\( \ \mathrm{R} \ \)を通るときに最小値を取ります。 ものさしでこの直線と平行な線を青い領域にずらしてみてください。切片はどんどん上に存在するようになるはずです。
こたえ
\( \ 48 \ \)円共有:
プロフィール
Author Profile