斜軸回転体のレシピを書いてみる。

2018年7月11日2023年1月15日積分とその応用実用数学技能検定（数学検定数検),数検準1級

読了時間: 約4分28秒

Lukia

回転体の基本的なイメージは、ぺらっぺらな円形のハムの中心に、金属の細い串（曲がらず硬い。断面は面積が測れないほどの小さな円形）を突き刺して、逆に肉の塊を作っていく。と考えるとよいと思います。
先端恐怖症の方は、イメージするだにブルッとするかもしれませんが、
目線を串の円形の断面が見えるほうに合わせると、ハムは円形ではあるものの、大きさ（つまり半径）が異なるハムがどんどん貫かれていきます。ハムの大きさは一定ではなく、面積が大きなハムや小さなハムが連なります。
この積み重ねを、串が長く見えるほうから見ると、でこぼこすると思います。

Lukia

さて、回転体を習い始めたころは、この串が$x$ 軸でした。
この串を90°回転させた $y$ 軸回転もありますが、これは式変形をすればなんとかなりますね。
しかし、中途半端に軸を45°回転させる「斜軸回転体」は、そう簡単ではありません。

Lukia

そこで、新たに $t$ 軸を設定し、
$t$ 軸について回転させていきます。

Lukia

目標は、$$\Large \frac{V}{\pi}=\int_0^\alpha PH^2 dt$$を導くことです。

問題

放物線 $ \ y=-x^2+x \ $ と直線 $ \ y=-x \ $ で囲まれた部分を、
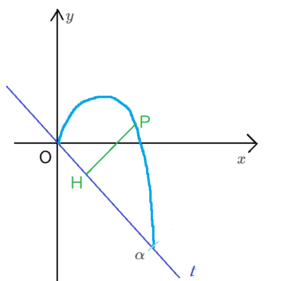
直線 $ \ y=-x \ $ のまわりに一回転してできる立体の体積 $ \ \mathrm{V} \ $ を求めよ。

Lukia

まずは、図形的なイメージをはっきりさせます。

$ \ y=-x^2+x \ $ を $ \ \mathrm{C} \ $ とし、 $ \ y=-x \ $ を $ \ l \ $ とする。
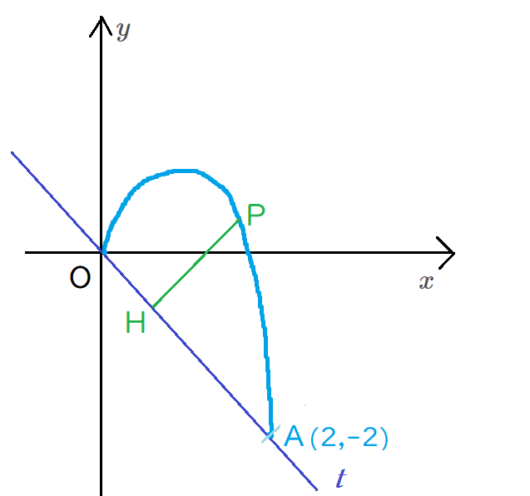
$ \ \mathrm{C} \ $ と $ \ l \ $ の交点は、 $ \ -x^2+x+x=0 \ $ より、
原点 $ \ \mathrm{O} \ $と点$ \ \mathrm{A}\left( 2,2\right) \ $である。
$ \ \mathrm{C} \ $ 上の任意の点を $ \ \mathrm{P}\left( x,-x^2+x\right) \ $とする。
点 $ \ \mathrm{P} \ $ から $ \ l \ $ におろした垂線の交点を $ \ \mathrm{H} \ $ とする。

Lukia

「点と直線の距離」を使って、PHの距離を求めます。

$$PH=\frac{\vert x-x^2+x \vert}{\sqrt{2}}=\frac{\vert -x^2+2x \vert}{\sqrt{2}}=\frac{-x^2+2x}{\sqrt{2}}$$

Lukia

なんで、簡単に絶対値がはずれてしまったのか。というのは、
グラフを描けばわかります。
$y=\vert -x^2+2x \vert$ のグラフは以下のとおり。

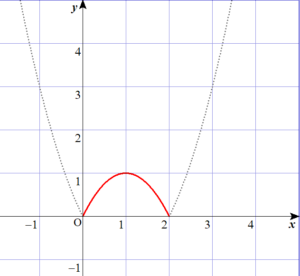
そして、今回は、定義域が $0 \lt x \lt 2$ となります。
赤い曲線が$x$ 軸よりも上にあります。
明らかに正ですね。

Lukia

斜軸回転体の問題は、結構難しいとされているので、
おそらく、$x $ 軸から $\pm 45$° 傾ける形が出題されると思います。
（これを必須で出題する数検は鬼ですね。）
つまり、直線は、$y=x　か、 y=-x$ に限定されるでしょう。
次の操作、点Qをおけるかおけないかで、
最後まで解答できるかどうかが分かれると思います。
今回のレシピのキモっちゃキモですね。

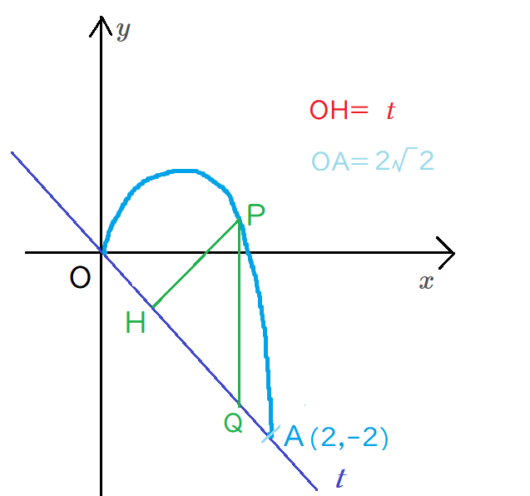
点 $ \ \mathrm{P} \ $ から $ \ x \ $ 軸におろした垂線と、$ \ l \ $ の交点を $ \ \mathrm{Q} \ $ とする。
$ \ \triangle \mathrm{PHQ} \ $ は、 $ \ \mathrm{PH}=\mathrm{PQ} \ $ の直角二等辺三角形であるから、
$ \ \mathrm{OH}=\mathrm{OQ}-\mathrm{QH}=\mathrm{OQ}-\mathrm{PH} \ $である。
$ \ \mathrm{OH}=t \ $ とすると、
$ \ t=\sqrt{2}x-\frac{\left( -x^2+2x\right)}{\sqrt{2}}=\frac{x^2}{\sqrt{2}} \ $

Lukia

両辺をについて微分し、目標の形に近づけていきます。

$$\begin{align}両辺を &x で微分する。 \\\\ \frac{dt}{dx}=&\frac{1}{\sqrt{2}}\cdot 2x より、 \\\\ dt=&\frac{2}{\sqrt{2}}x dx \end{align}$$

Lukia

直線 $l$ を $t$ 軸とみなし、回転体を求める式を立てます。
積分区間は、$OA$の長さが $2\sqrt{2}$ であることから、
$0$から $2\sqrt{2}$ となります。
また、計算している途中で、$\pi$ を書き忘れてしまう可能性があるので、
$\pi$ を左辺に避難させるようにしています。

$$\frac{V}{\pi}=\int_0^{2\sqrt{2}} PH^2 dt$$

Lukia

ここで、積分区間の変換（？）をしておきます。
私は、空いたスペースでこそッ。と計算してしまうので、通常解答には書きません。

$$\begin{align}t=&\frac{x^2}{\sqrt{2}} \\\\ \sqrt{2}t=&x^2\\\\ t=&2\sqrt{2} のとき、\\\\ 4=&x^2\\\\ただし、&0 \leq x \leq 2 であるから、\\\\ x=&2 \end{align}$$

$$\frac{V}{\pi}=\int_0^{2\sqrt{2}} PH^2 dt=\int_0^2 \left( \frac{-x^2+2x}{\sqrt{2}}\right)^2\cdot \frac{2}{\sqrt{2}} xdx$$
$$\begin{align} \frac{V}{\pi}&=\frac{1}{\sqrt{2}}\int_0^2 \left( x^5-4x^4+4x^3\right) dx\\\\ &=\frac{1}{\sqrt{2}}\left[ \frac{1}{6}x^6-\frac{4}{5}x^5+x^4\right]_0^2\\\\&=\frac{8\sqrt{2}}{15}\pi \end{align}$$
ゆえに、
$$\Large V=\frac{8\sqrt{2}}{15}\pi$$