外分を含む平面ベクトル（その2）【たすきがけで比を統一せよ!!】

Lukia

ベクトルにおいて、「外分」の考え方は少し難しい気がしてしまいますね。
（私もいまだに苦手です）
しかし、比の書き方をくふうすれば、内分と同じように扱うことができます。
単なる計算のためだけなら、今からご紹介する図の描き方でも十分対応します。

準備編

Lukia

「辺\( \ \mathrm{AB} \ \)を\( \ 8:3 \ \)に外分する」ということは、
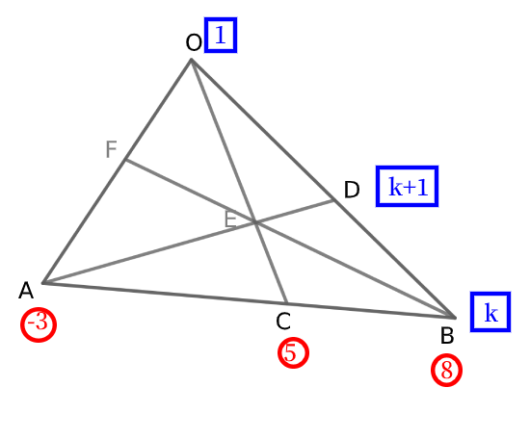
「辺\( \ \mathrm{AB} \ \)を\( \ 8:-3 \ \)に内分する」ともいえます。
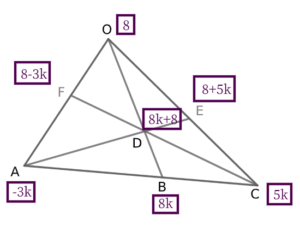
頂点と比をたすきがけ？するように、互い違いに書き込みます。

Lukia

ゆえに、頂点\( \ \mathrm{A} \ \)に\( \ −3 \ \),
頂点\( \ \mathrm{B} \ \)に\( \ 8 \ \)を書きます。
そして、\( \ \mathrm{A} \ \)と\( \ \mathrm{B} \ \)に書かれた比の和を内分点である\( \ \mathrm{C} \ \)に書きます。
今回は、\( \ -3+8=5 \ \)より\( \ 5 \ \)となりますね。

Lukia

辺\( \ \mathrm{OB} \ \)に関する内分もこれと同様におこないます。図では青い文字がそれにあたります。
（やり方は省略させてもらいますね）

Lukia

ここで、問題となってくるのが、頂点\( \ \mathrm{B} \ \)に\( \ \color{red}{8} \ \)と\( \ \color{#0004fc}{k} \ \)が書かれていることです。
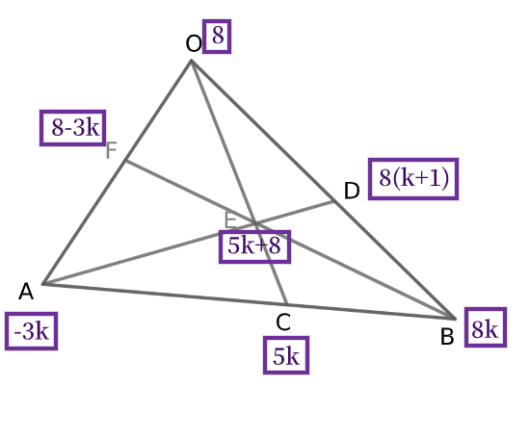
色を分けて書いているとおり、三角形\( \ \mathrm{OAB} \ \)としては内分比が統一されていません。
よって、赤い比のほうは\( \ \color{#0004fc}{k} \ \)倍し、
青い比のほうは\( \ \color{red}{8} \ \)倍して、内分比を統一します。

Lukia

ついでといってはなんですが、直線\( \ \mathrm{BE} \ \)と辺\( \ \mathrm{OA} \ \)の交点を\( \ \mathrm{F} \ \)とし、両端の比の和を書いておきます。

Lukia

点の上にすべて比をおくことができました。
準備は万端、早速問題を解いていきましょう。

(1)ベクトルOCを表す

Lukia

図に統一された比を書き込んでいるので、あとはそれを素直に書き出すだけです。

$$\begin{align}\overrightarrow{\mathrm{OC}}=&\displaystyle\frac{-3k\vec{a}+8k\vec{b}}{5k} \\\\ =&-\displaystyle\frac{3}{5}\vec{a}+\displaystyle\frac{8}{5}\vec{b}\end{align}$$

(2)t,sをkで表す

$$\begin{align}\overrightarrow{\mathrm{OE}}=&\displaystyle\frac{5k}{5k+8}\overrightarrow{\mathrm{OC}} \\\\ t=&\displaystyle\frac{5k}{5k+8} \end{align}$$

$$\begin{align}\overrightarrow{\mathrm{AE}}=&\displaystyle\frac{8k+8}{5k+8}\overrightarrow{\mathrm{AD}} \\\\ s=&\displaystyle\frac{8k+8}{5k+8} \end{align}$$

(3)とある条件を満たすときの定数kの値

Lukia

外分比を内分比に変換していますので、
この図では、\( \ \overrightarrow{\mathrm{BE}} \ \)が\( \ \overrightarrow{\mathrm{OA}} \ \)と平行になるイメージはどうやっても浮かびません。
しかし、単に計算して、定数\( \ k \ \)の値を求めるだけですから、図が正確である必要もないんですよね。

$$\begin{align}\overrightarrow{\mathrm{BE}}=&m\overrightarrow{\mathrm{OA}}\quad \left( mは実数\right) \quad とする.\\\\ \overrightarrow{\mathrm{OE}}-\overrightarrow{\mathrm{OB}}=&m\overrightarrow{\mathrm{OA}} \\\\ \displaystyle\frac{1}{5k+8}\left( -3k\vec{a}+8k\vec{b}\right)-\vec{b}=&m\vec{a} \end{align}$$
以上より
$$\begin{align}\displaystyle\frac{8k-5k-8}{5k+8}=&0 \\\\ 3k=&8 \\\\ k=&\displaystyle\frac{8}{3} \end{align}$$

Lukia

右辺には\( \ \vec{a} \ \)しかないのに、
左辺には\( \ \vec{a} \ \)だけでなく、\( \ \vec{b} \ \)も存在していますね。
右辺に\( \ \vec{b} \ \)がないことから、「以上より」以下の計算式が展開されます。

正しい位置に外分点を置いた図でも解いてみる。

Lukia

では、外分比を忠実に書き込む図のほうでも解いてみたいと思います。

Lukia

「辺\( \ \mathrm{AB} \ \)を\( \ 8:3 \ \)に外分する」ということは、「点\( \ \mathrm{A} \ \)から点\( \ \mathrm{B} \ \)の方向へ\( \ 8 \ \)進んで\( \ 3 \ \)戻ること」を意味しています。
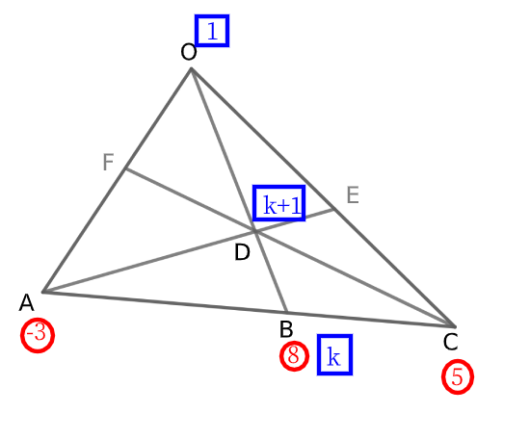
よって、点\( \ \mathrm{C} \ \)は、点\( \ \mathrm{A} \ \)から\( \ 8 \ \)離れた位置、さらに点\( \ \mathrm{B} \ \)とは\( \ 3 \ \)離れた位置に置かれることになります。

Lukia

しつこいようですが、
点\( \ \mathrm{C} \ \)は、線分\( \ \mathrm{AB} \ \)の内部ではなく、外部にありますね。
これが「外分点」といわれる所以です。

Lukia

注意してほしいのは、外分比の置き方ですね。
内分比と同様、比と点が互い違いになるように図に書き込むのですが、\( \ \mathrm{A}:\mathrm{B}=8:-3 \ \)と考えると、
点\( \ \mathrm{B} \ \)に書かれる比は、\( \ 8 \ \)ですからね。
点\( \ \mathrm{C} \ \)には\( \ 8+\left( -3\right)=5 \ \)として\( \ 5 \ \)を書き込みます。
ややこしいのは外分比の置き方だけなので、あとは、すでに示した図と同じく、比を統一していきます。（以下略とします）

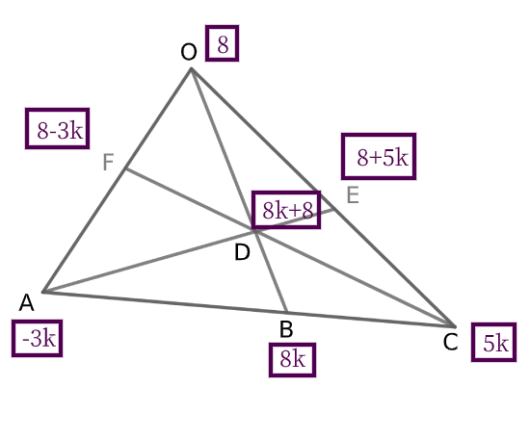
(1)
$$\begin{align}\overrightarrow{\mathrm{OC}}=&\displaystyle\frac{-3k\vec{a}+8k\vec{b}}{5k} \\\\ =&-\displaystyle\frac{3}{5}\vec{a}+\displaystyle\frac{8}{5}\vec{b} \end{align}$$

(2)
$$\begin{align}\overrightarrow{\mathrm{OE}}=&t\overrightarrow{\mathrm{OC}}=\displaystyle\frac{5k}{5k+8}\overrightarrow{\mathrm{OC}} \\\\ t=&\displaystyle\frac{5k}{5k+8} \end{align}$$
また、
$$\begin{align}\overrightarrow{\mathrm{AD}}=&\displaystyle\frac{5k+8}{8\left( k+1\right)}\overrightarrow{\mathrm{}}\overrightarrow{\mathrm{AE}}\quad より \\\\ \overrightarrow{\mathrm{AE}}=&\displaystyle\frac{8k+8}{5k+8}\overrightarrow{\mathrm{AD}} \\\\ s=&\displaystyle\frac{8k+8}{5k+8} \end{align}$$

(3)

Lukia

外分点を正しい位置に置いた図だと、\( \ AO//BE \ \)というのもイメージしやすいですね。

$$\begin{align}\overrightarrow{\mathrm{BE}}=&m\overrightarrow{\mathrm{OA}}\quad \left( mは実数\right)\quad とおく. \\\\ \overrightarrow{\mathrm{OE}}-\overrightarrow{\mathrm{OB}}=&t\overrightarrow{\mathrm{OC}}-\vec{b} \\\\ =&-\displaystyle\frac{3}{5}t\vec{a}+\displaystyle\frac{8}{5}t\vec{b}-\vec{b}\\\\ =&-\displaystyle\frac{3}{5}t\vec{a}\vec{a}+\left( \displaystyle\frac{8}{5}t-1\right)\vec{b}=m\vec{a} \end{align}$$
$$\begin{align}ここで& \ \displaystyle\frac{8}{5}t-1=0\quad より \\\\ \displaystyle\frac{8}{5}t=&1 \\\\ t=&\displaystyle\frac{5}{8} \end{align}$$

$$\begin{align}t=&\displaystyle\frac{5k}{5k+8}=\displaystyle\frac{5}{8} \\\\ 8k=&5k+8 \\\\ 3k=&8\\\\ k=&\displaystyle\frac{8}{3}\end{align}$$

こたえ

$$\begin{align}\left( 1\right)&\quad \overrightarrow{\mathrm{OC}}=\displaystyle\frac{-3\vec{a}+8\vec{b}}{5} \\\\ \left( 2\right)&\quad \quad s=\displaystyle\frac{8k+8}{5k+8}\quad ,\quad t=\displaystyle\frac{5k}{5k+8} \\\\ \left( 3\right)&\quad k=\displaystyle\frac{8}{3} \end{align}$$