中学数学の食塩水の濃度の問題(番外編:計算をくふうする)

読了時間: 約5分4秒
[mathjax]
中学数学は、めんどくささの端境期。

Lukia
今回は、番外編です。
計算のめんどくささでいえば、中学数学は小学校の算数に次ぐと思われます。
計算のめんどくささでいえば、中学数学は小学校の算数に次ぐと思われます。

もも
小学校は、計算のドリルとかいっぱいやっていましたもんね。

Lukia
計算力をつけさせるため。ということだと思いますけどね。
学年が上がるにつれて、より抽象的なことを考えなければならなくなるので、
そのぶん計算に手間取るようでは困るんですよね。
学年が上がるにつれて、より抽象的なことを考えなければならなくなるので、
そのぶん計算に手間取るようでは困るんですよね。

Lukia
低学年のうちに、機械的に手を動かせるようにしておけば、
高学年になって、抽象的な思考に頭を使えるようになります。
高学年になって、抽象的な思考に頭を使えるようになります。

Lukia
中学数学は、いわばその端境期で、
具体的に計算するのと、文字を使って抽象的に考えることをやらねばならないので、
結構大変なんですよね。
具体的に計算するのと、文字を使って抽象的に考えることをやらねばならないので、
結構大変なんですよね。

もも
高校では計算しないんですか?

Lukia
う~ん、まったくやらないわけではないのですが、ほとんど文字に置き換わっちゃいますね。
たとえば、小学校で円の面積というと、
半径5センチならば、
\(\Large 5\times 5\times 3.14\) と式を立てて計算します。
ちなみに、答えは78.5㎠です。
たとえば、小学校で円の面積というと、
半径5センチならば、
\(\Large 5\times 5\times 3.14\) と式を立てて計算します。
ちなみに、答えは78.5㎠です。

Lukia
中学生になると、円周率は、π(パイ)に置き換えられるので、
同じ問題でも、\(\Large 5\times 5\times \pi=25\pi\) と式を立て、
25π㎠と答えればよいことになります。
同じ問題でも、\(\Large 5\times 5\times \pi=25\pi\) と式を立て、
25π㎠と答えればよいことになります。

もも
なるほど。

Lukia
高校数学になると、半径5センチなんて、数や単位がついていることはまれで、
半径を r とする。なんてことに。
ゆえに、 \(\Large \pi r^2\)と表されます。
半径を r とする。なんてことに。
ゆえに、 \(\Large \pi r^2\)と表されます。

もも
うわ~、「5センチ」が消えてる!

Lukia
はい。高校数学だと、式は立てておくから、
必要なら r に「5センチ」を入れなさいよ。というスタンスに変わるんですね。
必要なら r に「5センチ」を入れなさいよ。というスタンスに変わるんですね。

もも
計算しなくていいのは、楽そうでいいけれど、
具体的なイメージがわきにくいですね。
具体的なイメージがわきにくいですね。

Lukia
まぁ、そうともいえますね。
高校数学では具体的な数を計算することは減るのですが、
逆に理科、特に化学は計算量が増えます。
高校数学では具体的な数を計算することは減るのですが、
逆に理科、特に化学は計算量が増えます。

もも
ひえぇ。

Lukia
濃度に関する計算は、結構ガッツリ出ますよ。

もも
のの~・・・(汗)

Lukia
前置きが長くなりましたが、分数や小数点の計算などが苦手な人のために、
こんな計算のくふうはいかがですか?という提案をしてみたいと思います。
こんな計算のくふうはいかがですか?という提案をしてみたいと思います。
問題
質量パーセント濃度が8%の食塩水において、食塩が10g含まれている食塩水の重さは何gか。
表に書き込む。

もも
いつもの表を描きますか?
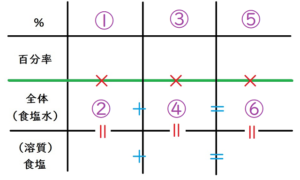

Lukia
そうですね。しかし、今回は、1種類の食塩水だけなので、
横長の線を3等分するように、縦の線を2本引きましょう。
横長の線を3等分するように、縦の線を2本引きましょう。

Lukia
今回は、「計算のくふう」に重点をおきたいので、
数字を書き込んだ表を示しますね。
数字を書き込んだ表を示しますね。
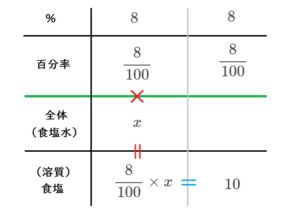
計算してみる。

Lukia
ここからは、ふきだしなしで書いていきますね。
表より式を立てます。
$$\Large \frac{8}{100}\times x=10$$
すなわち、
$$\Large \frac{8}{100}x=10$$
を解きます。
まず、両辺の分子を約分します。
すると、
$$\Large \frac{4}{100}x=5$$
となりますね。

すると、
$$\Large \frac{100}{100}x=5\times 25$$
すなわち、
$$\Large x=125$$
が導かれます。
分母の100はできるだけ最後まではらわない。

もも
わぁっ、左辺が\(\Large \frac{100}{100}\) となって、簡単に消えちゃいましたね。

Lukia
計算するときに、分母があると大変ですよね。
しかし、もし分母が、100とか1000などのような、きれいな数というか、きりのいい数字だったら、
あんまり動かさないほうがいいのです。
しかし、もし分母が、100とか1000などのような、きれいな数というか、きりのいい数字だったら、
あんまり動かさないほうがいいのです。

もも
たしかに、両辺に100をかけて。とか、
\(\Large x\)について解く。などの方法がありますけど、
分数を反対の辺に移動させるときは、逆数にしなくちゃ。とか思うと、
それだけでエネルギー奪われる気がしますね。
\(\Large x\)について解く。などの方法がありますけど、
分数を反対の辺に移動させるときは、逆数にしなくちゃ。とか思うと、
それだけでエネルギー奪われる気がしますね。

Lukia
まず、=(イコール)でつながれているのなら、
両辺に同じ操作をしてやらなければならないことは覚えておいてくださいね。
左辺に何かを足したなら、右辺にも同じものを足してやらねばならないし、
左辺を何かで割ったなら、右辺も同じもので割ってやらねばなりません。
両辺に同じ操作をしてやらなければならないことは覚えておいてくださいね。
左辺に何かを足したなら、右辺にも同じものを足してやらねばならないし、
左辺を何かで割ったなら、右辺も同じもので割ってやらねばなりません。

Lukia
こういう操作は高校数学でもよくやるんですよね。
たとえば、分子分母に同じものをかける。とかね。
たとえば、分子分母に同じものをかける。とかね。

もも
分子分母に同じもの?

Lukia
たとえばこんな感じですかね。
例題1
$$\Large \sin \theta=\sin 2\times \frac{\theta}{2}$$

Lukia
アルファベット部分は無視してもらっていいのですが、
\(\Large \theta=\frac{2}{2}\theta\) といってもさしつかえないでしょ?
ちなみに、 \(\Large \theta\) は、「シータ」と読みます。
\(\Large \theta=\frac{2}{2}\theta\) といってもさしつかえないでしょ?
ちなみに、 \(\Large \theta\) は、「シータ」と読みます。

もも
分子と分母が同じ数なら、1となるし、
\(\Large 1\theta\) とは書かずに、\(\Large \theta\) と書く。というルールがありますもんね。
\(\Large 1\theta\) とは書かずに、\(\Large \theta\) と書く。というルールがありますもんね。
例題2

Lukia
たとえば、 \(\Large \frac{1.1}{4}\) を計算し、小数第3位を四捨五入して答えよ。
なんて問題が出たらどうします?
なんて問題が出たらどうします?

もも
\(\Large 1.1÷4\) をする・・・かな。

Lukia
どうせ計算しなくちゃいけないなら、わり算よりかけ算のほうが楽です。
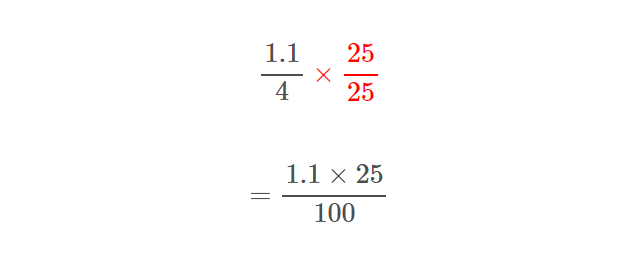
分子の小数点がうっとうしいので、
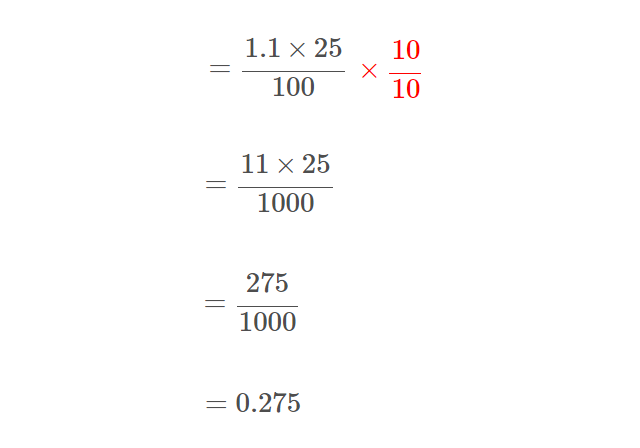
小数第3位を四捨五入して、
$$\Large 0.28$$

もも
ホントだ。場合によっては、わり算のほうが早いかもしれないけど、
気分的にはかけ算のほうが楽ですね。
気分的にはかけ算のほうが楽ですね。
コロンブスの卵

Lukia
どんなに気をつけても、人間はミスをします。
小数点の位置の間違いなんて、大人でもやっちゃいますからね。
高校化学では、ものすご~く小さい世界のことを計算させたりするので、
ギリッギリまで小数点をいじらないようにするくふうが必要になるんです。
小数点の位置の間違いなんて、大人でもやっちゃいますからね。
高校化学では、ものすご~く小さい世界のことを計算させたりするので、
ギリッギリまで小数点をいじらないようにするくふうが必要になるんです。

Lukia
高校数学でも、例題1のように、
どうせ1になるんだから、\(\Large \frac{2}{2}\) をかけてもいいでしょ。というようなものがちょいちょい出てきます。
どうせ1になるんだから、\(\Large \frac{2}{2}\) をかけてもいいでしょ。というようなものがちょいちょい出てきます。

もも
そうなんですねぇ。

Lukia
そんなやりかたずるいだろ!とというか、
あっちゃ~、やられた~!と思わされることが結構ありますね。
わたしにとっては、「コロンブスの卵」みたいなもんです。
あっちゃ~、やられた~!と思わされることが結構ありますね。
わたしにとっては、「コロンブスの卵」みたいなもんです。

もも
たしかに、文字ばっかりの式を立てていると、
案外こういう「あたりまえ」のことに気づけなくなるのかもしれませんね。
案外こういう「あたりまえ」のことに気づけなくなるのかもしれませんね。

Lukia
ホント、中学生なのに、よくわかってますねぇ。
誰が生み出したんだか・・・。
誰が生み出したんだか・・・。
[subscribe2]










ディスカッション
コメント一覧
まだ、コメントがありません