中学数学の食塩水に塩を混ぜる問題（その1）
読了時間: 約3分49秒
[mathjax]
Lukia
これまでは、2種類の食塩水を混ぜ合わせる問題を解いてきましたが、
今回からは、食塩水と食塩を混ぜ合わせる問題を解いていきたいと思います。
これまでどおり表を使っていきますので、気楽にとりくんでくださいね。
今回からは、食塩水と食塩を混ぜ合わせる問題を解いていきたいと思います。
これまでどおり表を使っていきますので、気楽にとりくんでくださいね。
問題
4%の食塩水600gに食塩を加えて20%の食塩水を作った。
加えた食塩は何gか。
加えた食塩は何gか。
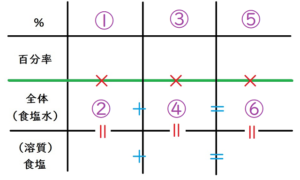
表に書き込む。
もも
これまでどおり、横長の線を3本、それを4等分できるように縦の線を3本描いて、表を作成していいですか？
Lukia
そうですね。お願いします。
ももちゃんは、以下のような表を描いています。
ももちゃんは、以下のような表を描いています。
もも
ということは、わかっている数字を書き込んでいくのも、手順としては同じですね。
じゃ、書き込んでみようっと。
①が4、
②が600・・・
じゃ、書き込んでみようっと。
①が4、
②が600・・・
もも
③は？
Lukia
ここで、さっそくなのですが、「食塩水に『塩』を混ぜ合わせる」問題のポイントをおさえていきます。
Lukia
ももちゃん。たとえば。なのですが、
100ｇの食塩には、何gの食塩が含まれていますか？
100ｇの食塩には、何gの食塩が含まれていますか？
もも
100ｇの食塩に、何gの食塩？
・・・100ｇです。
・・・100ｇです。
Lukia
そのとおり。
では、もう少し変なことを聞きます。
では、もう少し変なことを聞きます。
Lukia
その場合、食塩は、全体の何%をしめていますか？
もも
全体の重さが100ｇで、そのうち食塩は100ｇなんだから・・・
もも
100％です！
Lukia
そう。つまり、食塩水に「食塩」を混ぜ合わせるとき、
「食塩」の濃度は、100％と考えていいんですね。
だから、③には、100が入ります。
ポイントはここだけで、あとはこれまでと変わりません。
「食塩」の濃度は、100％と考えていいんですね。
だから、③には、100が入ります。
ポイントはここだけで、あとはこれまでと変わりません。
もも
そうなんだ～！
じゃ、③は100、
④は、問題文からするとわからない（ここを求める）ようだから、ほっておこう。
いや、もう
そして、⑤が20ですね。
じゃ、③は100、
④は、問題文からするとわからない（ここを求める）ようだから、ほっておこう。
いや、もう
そして、⑤が20ですね。
Lukia
「食塩」の濃度を100とおく以外は、特に目新しいものはないので、
ももちゃんはどんどん手を動かせているようです。
ももちゃんはどんどん手を動かせているようです。
もも
はい。
②と④がわかっているので、「横はたし算」ができますね。
②+④=⑥だから、
⑥は
②と④がわかっているので、「横はたし算」ができますね。
②+④=⑥だから、
⑥は
％を百分率に直しておく。
もも
いつもの手順だから、もうやっちゃいますね。
左から、
左から、
縦はかけ算・横はたし算
Lukia
はやッ！
少しはしゃべる余地を残しておいてほしいですよ。（ブツブツ・・・）
まぁ、たくさん問題解いてきているから、慣れた証拠ですね。
それでは、「縦はかけ算」をして、一番下の段に書き込むのをお願いします。
少しはしゃべる余地を残しておいてほしいですよ。（ブツブツ・・・）
まぁ、たくさん問題解いてきているから、慣れた証拠ですね。
それでは、「縦はかけ算」をして、一番下の段に書き込むのをお願いします。
もも
は～い。
じゃ、食塩水の列の「縦はかけ算」をします。
じゃ、食塩水の列の「縦はかけ算」をします。
もも
次に、食塩の列。
Lukia
式を立ててから一気に消すため、このままにしておいてください。
もも
は～い。
じゃ、最後に、できあがりの食塩水の列。
じゃ、最後に、できあがりの食塩水の列。
一番下の段の「たし算」をする。
Lukia
「縦はかけ算」をしたことによって、一番下の段のマスがすべて埋まりました。
では、「横はたし算」をして、式を立ててください。
では、「横はたし算」をして、式を立ててください。
もも
は～い。
式は、
式は、
Lukia
はい。それでは、計算をしていきましょうね。
以下は、ふきだしを外します。
以下は、ふきだしを外します。
両辺の分母をはらい、展開します。
左辺にx、右辺に600でまとめます。
もも
つまり、混ぜ合わせた「食塩」は120ｇということになりますね。
Lukia
正解です。
こたえ
Lukia
いかがですか。
「食塩」そのものの濃度をどう考えるか。というポイントをおさえれば、
難しい問題ではなかったと思います。
いまのところ、見つけている問題は、あと一問ぐらいなので、
「食塩水に『食塩』を混ぜ合わせる」問題は、次が最終回となる予定です。
「食塩」そのものの濃度をどう考えるか。というポイントをおさえれば、
難しい問題ではなかったと思います。
いまのところ、見つけている問題は、あと一問ぐらいなので、
「食塩水に『食塩』を混ぜ合わせる」問題は、次が最終回となる予定です。
120g
共有:
プロフィール
Author Profile
